题目内容
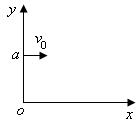
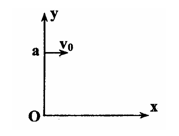
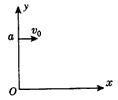
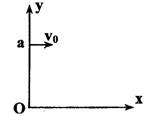
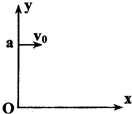如图所示，a点距坐标原点的距离为L，坐标平面内有边界过a点和坐标原点0的圆形匀强磁场区域，磁场方向垂直坐标平面向里．有一电子（质量为m、电荷量为e）从a点以初速度v0平行x轴正方向射入磁场区域，在磁场中运行，从x轴上的b点（图中未画出）射出磁场区域，此时速度方向与x轴的正方向之间的夹角为60°，求（1）磁场的磁感应强度
（2）磁场区域的圆心O1的坐标
（3）电子在磁场中运动的时间．
分析：（1）根据题意正确画出粒子运动的轨迹，找出R与L之间的关系，由洛伦兹力提供向心力的方程可得；
（2）由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点；
（3）粒子在磁场中飞行时间为弧度比速度．
（2）由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点；
（3）粒子在磁场中飞行时间为弧度比速度．
解答：
解：（1）粒子运动的轨迹如图得R=2L
又，洛伦兹力提供向心力，得：eBv0=
所以：B=
=
（2）由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点．所以：
x轴坐标x=aO1sin60°=
L
y轴坐标为y=L-aO1sin60°=
O1点坐标为（
L，
）
（3）粒子在磁场中飞行时间为：t=
=
答：（1）磁场的磁感应强度B=
；
（2）磁场区域的圆心O1的坐标（
L，
）
（3）电子在磁场中运动的时间t=
．
解：（1）粒子运动的轨迹如图得R=2L又，洛伦兹力提供向心力，得：eBv0=
m
| ||
| R |
所以：B=
| mv0 |
| eR |
| mv0 |
| 2eL |
（2）由题意和上图的几何关系可得，过a、O、B三点的圆的圆心在aB连线的中点．所以：
x轴坐标x=aO1sin60°=
| ||
| 2 |
y轴坐标为y=L-aO1sin60°=
| L |
| 2 |
O1点坐标为（
| ||
| 2 |
| L |
| 2 |
（3）粒子在磁场中飞行时间为：t=
| Rθ |
| v0 |
| 2πL |
| 3v0 |
答：（1）磁场的磁感应强度B=
| mv0 |
| 2eL |
（2）磁场区域的圆心O1的坐标（
| ||
| 2 |
| L |
| 2 |
（3）电子在磁场中运动的时间t=
| 2πL |
| 3v0 |
点评：该类题目根据题意正确画出粒子运动的轨迹，找出R与L之间的关系，是解决问题的关键．
练习册系列答案
相关题目
