题目内容
（2013?开封一模）选修3-3模块如图所示，一个上下都与大气相通的直圆筒，中间用两个活塞A与B封住一定质量的理想气体，A，B都可沿圆筒无摩擦地上、下滑动，但不漏气．A的质量可不计，B的质量为M，并与一劲度系数k=5×103N/m的较长的弹簧相连，已知大气压强p0=1×105Pa，活塞的横截面积s=0.01m2．平衡时，两活塞问的距离l0=0.6m，现用力压A，使之缓慢向下移动一定距离后，保持平衡，此时，用于压A的力F=5×102N，求活塞A向下移动的距离．（假定气体温度保持不变）分析：由于A的质量可不计，初态时，封闭气体的压强等于大气压，以B为研究对象，求出弹簧的压缩量．当用力压A时，再以B为研究对象，求出弹簧的弹力，由胡克定律求出弹簧的压缩量，根据玻意耳定律求出活塞A向下移动的距离．
解答：解：设活塞A向下移动l，相应B向下移动x，对气体分析：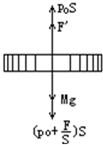
初态：p1=p0 V1=l0S
末态：p2=p0+
V2=（l0-1+x）S
由玻-意耳定律：p1V1=p2V2
因为两活塞间的距离原来为l0，活塞A向下移动l，相应B向下移动x，则末状态时，两活塞的距离为l0-l+x．
得：p1l0S=（p0+
）（l0-1+x ）S…①
初态时，弹簧被压缩量为x'，由胡克定律：Mg=kx'…②
当活塞A受到压力F时，活塞B的受力情况如图所示．F'为此时弹簧弹力
由平衡条件可知p0S+F'=p0S+F+Mg…③
由胡克定律有：F'=k（x+x'）…④
联立①②③④解得：l=0.3m．
答：活塞A向下移动的距离为0.3m．
初态：p1=p0 V1=l0S
末态：p2=p0+
| F |
| S |
由玻-意耳定律：p1V1=p2V2
因为两活塞间的距离原来为l0，活塞A向下移动l，相应B向下移动x，则末状态时，两活塞的距离为l0-l+x．
得：p1l0S=（p0+
| F |
| S |
初态时，弹簧被压缩量为x'，由胡克定律：Mg=kx'…②
当活塞A受到压力F时，活塞B的受力情况如图所示．F'为此时弹簧弹力
由平衡条件可知p0S+F'=p0S+F+Mg…③
由胡克定律有：F'=k（x+x'）…④
联立①②③④解得：l=0.3m．
答：活塞A向下移动的距离为0.3m．
点评：本题考查了玻意耳定律与力学知识的综合，有一定难度．关键搞清初末状态，运用力学平衡和玻意耳定律综合求解．
练习册系列答案
相关题目
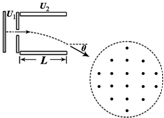（2013?开封一模）如图所示，一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C，从静止开始经电压为U1=100V的电场加速后，水平进入两平行金属板间的偏转电场中，微粒射出电场时的偏转角θ=60°，并接着沿半径方向进入一个垂直纸面向外的圆形匀强磁场区域，微粒射出磁场时的偏转角也为θ=60°．已知偏转电场中金属板长L=2
（2013?开封一模）如图所示，在垂直纸面向里、磁感应强度为B的匀强磁场区域中，有一个均匀导线制成的单匝直角三角形线框，现用外力使线框以恒定的速度v沿垂直磁场方向向右运动，运动中线框的AB边始终与磁场右边界平行．已知AB=BC=l，线框导线的总电阻为R，则线框离开磁场的过程中（ ）