题目内容
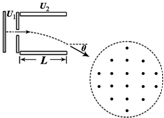 (2013?开封一模)如图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场中,微粒射出电场时的偏转角θ=60°,并接着沿半径方向进入一个垂直纸面向外的圆形匀强磁场区域,微粒射出磁场时的偏转角也为θ=60°.已知偏转电场中金属板长L=2
(2013?开封一模)如图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场中,微粒射出电场时的偏转角θ=60°,并接着沿半径方向进入一个垂直纸面向外的圆形匀强磁场区域,微粒射出磁场时的偏转角也为θ=60°.已知偏转电场中金属板长L=2| 3 |
| 3 |
(1)带电微粒经U1=100V的电场加速后的速率;
(2)两金属板间偏转电场的电场强度E;
(3)匀强磁场的磁感应强度的大小.
分析:(1)根据动能定理求解带电微粒经U1=100V的电场加速后的速率;
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动,运用运动的分解法研究:在水平方向微粒做匀速直线运动,在竖直方向做匀加速直线运动,根据牛顿第二定律和运动学公式结合求解电场强度.
(2)带电微粒进入磁场后做匀速圆周运动,轨迹对应的圆心角就等于速度的偏向角,作出轨迹,得到轨迹的圆心角,由几何知识求出轨迹半径,由牛顿第二定律求解磁感应强度的大小.
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动,运用运动的分解法研究:在水平方向微粒做匀速直线运动,在竖直方向做匀加速直线运动,根据牛顿第二定律和运动学公式结合求解电场强度.
(2)带电微粒进入磁场后做匀速圆周运动,轨迹对应的圆心角就等于速度的偏向角,作出轨迹,得到轨迹的圆心角,由几何知识求出轨迹半径,由牛顿第二定律求解磁感应强度的大小.
解答:解:(1)带电微粒经加速电场加速后速度为v1,
根据动能定理:qU1=
m
得:v1=
=1.0×104m/s 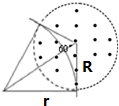
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动.在水平方向微粒做匀速直线运动.
水平方向:v1=
带电微粒在竖直方向做匀加速直线运动,加速度为a,出电场时竖直方向速度为v2
竖直方向:a=
由几何关系:tanθ=
,由题θ=60°
解得:E=10000V/m.
(3)设带电粒子进磁场时的速度大小为v,则:v=
=2×104m/s
由粒子运动的对称性可知,入射速度方向过磁场区域圆心,则出射速度反向延长线过磁场区域圆心,粒子在磁场中的运动轨迹如图所示,则轨迹半径为:r=Rtan60°=0.3m
由:qvB=m
得:B=
=0.13T
答:(1)带电微粒经U1=100V的电场加速后的速率是1.0×104m/s;
(2)两金属板间偏转电场的电场强度E是10000V/m;
(3)匀强磁场的磁感应强度的大小是0.13T.
根据动能定理:qU1=
| 1 |
| 2 |
| v | 2 1 |
得:v1=
|

(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动.在水平方向微粒做匀速直线运动.
水平方向:v1=
| L |
| t |
带电微粒在竖直方向做匀加速直线运动,加速度为a,出电场时竖直方向速度为v2
竖直方向:a=
| qE |
| m |
由几何关系:tanθ=
| v2 |
| v1 |
解得:E=10000V/m.
(3)设带电粒子进磁场时的速度大小为v,则:v=
| v1 |
| cos60° |
由粒子运动的对称性可知,入射速度方向过磁场区域圆心,则出射速度反向延长线过磁场区域圆心,粒子在磁场中的运动轨迹如图所示,则轨迹半径为:r=Rtan60°=0.3m
由:qvB=m
| v2 |
| r |
得:B=
| mv |
| qr |
答:(1)带电微粒经U1=100V的电场加速后的速率是1.0×104m/s;
(2)两金属板间偏转电场的电场强度E是10000V/m;
(3)匀强磁场的磁感应强度的大小是0.13T.
点评:本题的难点是作出粒子的运动轨迹,根据几何知识得到轨迹半径与磁场边界半径的关系.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2013?开封一模)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑.现将一质量为m,带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
(2013?开封一模)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑.现将一质量为m,带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( ) (2013?开封一模)如图所示,有一个等腰直角三角形的匀强磁场区域,其直角边长为L,磁场方向垂直纸面向外,磁感应强度大小为B.一边长为L总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁 场区域.取沿a→b→c→d→a的感应电流为正,则表示线框中电流i随bC边的位置坐标x变化的图象正确的是( )
(2013?开封一模)如图所示,有一个等腰直角三角形的匀强磁场区域,其直角边长为L,磁场方向垂直纸面向外,磁感应强度大小为B.一边长为L总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁 场区域.取沿a→b→c→d→a的感应电流为正,则表示线框中电流i随bC边的位置坐标x变化的图象正确的是( ) (2013?开封一模)如图所示K与虚线MN之间是加速电场.虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行.电场和磁场的方向如图所示.图中A点与O点的连线垂直于荧光屏.一带正电的粒子由静止被加速从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在图中的荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=
(2013?开封一模)如图所示K与虚线MN之间是加速电场.虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行.电场和磁场的方向如图所示.图中A点与O点的连线垂直于荧光屏.一带正电的粒子由静止被加速从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在图中的荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U= (2013?开封一模)如图所示,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器滑片P向左移动,则( )
(2013?开封一模)如图所示,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器滑片P向左移动,则( ) (2013?开封一模)如图所示为一传送带装置,其中AB段是水平的,长度LAB=5m,倾角为θ=37°,AB和BC在B点通过一段极短的圆弧连接(图中未画出圆弧),传送带以的恒定速率v=4m/s顺时针运转.已知工件与传送带间的动摩擦因数μ=0.5,重力加速度g=l0m/s2.现将一个工件(可看作质点)无初速地放在A点,求:
(2013?开封一模)如图所示为一传送带装置,其中AB段是水平的,长度LAB=5m,倾角为θ=37°,AB和BC在B点通过一段极短的圆弧连接(图中未画出圆弧),传送带以的恒定速率v=4m/s顺时针运转.已知工件与传送带间的动摩擦因数μ=0.5,重力加速度g=l0m/s2.现将一个工件(可看作质点)无初速地放在A点,求: