题目内容
14.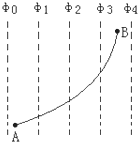 如图所示,实线AB为一电子在电场中的运动轨迹,虚线为等势线且相邻两等势线间的电势差相等、距离相等,电子运动到等势线φ1上时,具有动能3.0×10-20J,它运动到等势线φ3上时,具有动能1.0×1.0-20J.令φ0=0,电子重力不计,则下列说法正确的是( )
如图所示,实线AB为一电子在电场中的运动轨迹,虚线为等势线且相邻两等势线间的电势差相等、距离相等,电子运动到等势线φ1上时,具有动能3.0×10-20J,它运动到等势线φ3上时,具有动能1.0×1.0-20J.令φ0=0,电子重力不计,则下列说法正确的是( )| A. | 电场方向水平向左 | |
| B. | 电子在运动过程中加速度变小 | |
| C. | 当该电子的电势能为4×10-21J时,其动能大小为3.6×10-20J | |
| D. | 电子在A点的电势能为负值 |
分析 根据动能的变化,判断电势能的变化,得出电势的高低,根据电场线与等势面垂直,且指向电势低的等势面,判断电场的方向;该电场是匀强电场,电子所受的电场力不变,加速度不变;根据电势能公式Ep=qφ,分析电子在A点的电势能;根据动能定理和电场的特点,求出电子在A处的动能,得到总能量,由能量守恒求解电势能为4×10-21JJ时的动能.
解答 解:A、据题电子从A到B,动能减小,则电势能增大,而电子带负电,电子在电势低处电势能大,所以φ1>φ3,因此电场方向水平向右,故A错误.
B、相邻两等势线间的电势差相等、距离相等,由公式$\frac{U}{d}$可知该电场是匀强电场,电子所受的电场力不变,加速度不变,故B错误.
C、电子从等势线φ1运动到等势线φ3时,动能减小2×10-20J,由动能定理可知电场力做功 W13=2×10-20J.由于相邻等势面间电势差相等,根据W=qU可知,电子从等势线φ0运动到等势线φ3时,电场力做功应为W03=-3×10-20J,动能减小-3×10-20J,所以电子在A处的动能为 EkA=4×10-20J,总能量为E=EkA+EpA=4×10-20J,根据能量守恒可得当该电子的电势能为4×10-21J时,其动能大小为3.6×10-20J,故C正确.
D、令φ0=0,则A点电势为负,由公式Ep=qφ可知电子在A点的电势能为正.故D错误.
故选:C
点评 学习电场中的功能关系时可以类比重力场中的功能关系,如只有重力做功,动能和电势能之和保持不变;要知道只有电场力做功,电势能和动能之和保持不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图是交流发电机的示意图.线圈abcd在磁场中匀速转动产生交流电.线圈的ab边和cd边连在两个金属滑环上,两个滑环通过金属片做的电刷和外电路相连.当线圈沿逆时针方向转动时,以下判断正确的是( )
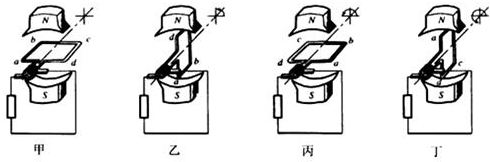

| A. | 当线圈转动图甲、图丙的位置时,穿过线圈的磁通量的变化率最大 | |
| B. | 当线圈转动图乙、图丁的位置时,穿过线圈的磁通量的变化率最大 | |
| C. | 当线圈转到图乙的位置时,线圈中的电流方向为d→c→b→a→d | |
| D. | 当线圈转到图丁的位置时,线圈中的电流方向为d→c→b→a→d |
9.A、B两个电阻的伏安特征曲线如图所示,下列判断正确的是( )


| A. | 图线表示电阻与电压成正比 | B. | 图线表示电阻与电流成反比 | ||
| C. | A的阻值小于B的阻值 | D. | A的阻值大于B的阻值 |
19.甲、乙两个质点同时同地向做直线运动,它们的v-t图象如图所示,则( )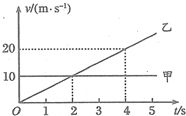

| A. | 乙的加速度不断增大 | B. | 4s末乙追上甲 | ||
| C. | 在4s内甲的速度大于乙的平均速度 | D. | 乙追上甲时距离出发点20m |
6.一辆公共汽车进站后开始刹车.做匀减速直线运动,开始刹车后的第1s内和第3s内位移大小依次为13m和9m,则刹车后6s内的位移是( )
| A. | 48 m | B. | 24 m | C. | 25 m | D. | 75 m |
3.关于电容器,以下说法正确的是( )
| A. | 电容器两板正对面积变大,电容变小 | |
| B. | 电容器两板距离变大,电容变大 | |
| C. | 两板间放入电介质,电容变大 | |
| D. | 两板间电压增大,电容变大 |
4.有下列①、②、③、④所述的四种情景,请根据所学知识从A、B、C、D四个选项中选择对情景的分析和判断的正确说法( )
①点火后即将升空的火箭;
②高速公路上沿直线高速行驶的轿车为避免事故紧急刹车;
③运行的磁悬浮列车在轨道上高速行驶;
④太空的空间站在绕地球匀速转动.
①点火后即将升空的火箭;
②高速公路上沿直线高速行驶的轿车为避免事故紧急刹车;
③运行的磁悬浮列车在轨道上高速行驶;
④太空的空间站在绕地球匀速转动.
| A. | 因火箭还没运动,所以加速度一定为零 | |
| B. | 轿车紧急刹车,速度变化很快,所以加速度很大 | |
| C. | 高速行驶的磁悬浮列车,因速度很大,所以加速度也一定很大 | |
| D. | 空间站做匀速转动,不能当成质点 |
