Question

【题目】如图所示，平行金属导轨与水平面间夹角均为37°，导轨间距为 1 m，电阻不计，导轨足够长．两根金属棒ab和a′b′的质量都是0.2 kg，电阻都是1 Ω，与导轨垂直放置且接触良好，金属棒和导轨之间的动摩擦因数为0.25，两个导轨平面处均存在着垂直轨道平面向上的匀强磁场(图中未画出)，磁感应强度B的大小相同．让a′b′固定不动，将金属棒ab由静止释放，当ab下滑速度达到稳定时，整个回路消耗的电功率为8 W．求：

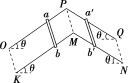
(1)ab下滑的最大加速度；

(2)ab下落了30 m高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量Q为多大？

(3)如果将ab与a′b′同时由静止释放，当ab下落了30 m高度时，其下滑速度也已经达到稳定，则此过程中回路电流的发热量Q′为多大？(g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8)

Answer 1

【答案】(1)4 m/s2 (2)30 J (3)75 J

【解析】(1)当ab棒刚下滑时，ab棒的加速度有最大值：

a＝gsin θ－μgcos θ＝4 m/s2.

(2)ab棒达到最大速度时做匀速运动，有

mgsin θ＝BIL＋μmgcos θ，

整个回路消耗的电功率

P电＝BILvm＝(mgsin θ－μmgcos θ)vm＝8 W，

则ab棒的最大速度为：vm＝10 m/s

由P电＝＝

得：B＝0.4 T.

根据能量守恒得：mgh＝Q＋mv＋μmgcos θ·

解得：Q＝30 J.

(3)由对称性可知，当ab下落30 m稳定时其速度为v′，a′b′也下落30 m，其速度也为v′，ab和a′b′都切割磁感线产生电动势，总电动势等于两者之和．

根据共点力平衡条件，对ab棒受力分析，

得mgsin θ＝BI′L＋μmgcos θ

又I′＝＝

解得v′＝5 m/s

由能量守恒得：

2mgh＝×2mv′2＋2μmgcos θ·＋Q′

代入数据得Q′＝75 J.