题目内容
【题目】如图所示,AB和CD为两个对称斜面,其上部足够长,下部分分别与一个光滑的圆弧面的两端相切,圆弧圆心角为120°,半径R=2.0m,一个质量为m=1kg的物体在离弧高度为h=3.0m处,以初速度4.0m/s沿斜面运动,若物体与两斜面间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则
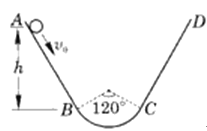
(1)物体在斜面上(不包括圆弧部分)走过路程的最大值为多少?
(2)试描述物体最终的运动情况.
(3)物体对圆弧最低点的最大压力和最小压力分别为多少?
【答案】(1)38m(2)物体最终是在B、C之间的圆弧上来回做变速圆周运动,且在B、C点时速度为零.
(3)Nmax=54.5N;Nmin=20N.
【解析】(1)物体在两斜面上来回运动时,克服摩擦力所做的功Wf=μmgcos60°·s总.
物体从开始直到不再在斜面上运动的过程中mgh-Wf=0-![]() mv02.解得s总=38m.
mv02.解得s总=38m.
(2)物体最终是在B、C之间的圆弧上来回做变速圆周运动,且在B、C点时速度为零.
(3)物体第一次通过圆弧最低点时,圆弧所受压力最大.由动能定理得
mg[h+R(1-cos60°)]-μmg![]() =
=![]() m(v12-v02)
m(v12-v02)
由牛顿第二定律得Nmax-mg=![]() ,
,
解得Nmax=54.5N.
物体最终在圆弧上运动时,圆弧所受压力最小.由动能定理得
mgR(1-cos60°)=![]() mv22
mv22
由牛顿第二定律得Nmin-mg=![]() 解得Nmin=20N.
解得Nmin=20N.

练习册系列答案
相关题目