题目内容
11.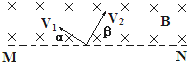 如图所示.直线MN上方垂直纸面向里的、磁感应强度为B的匀强磁场,质量为m、带电量为-q(q>0)的粒子1在纸面内以速度V1=V0从O点射入磁场,其射入方向与MN的夹角α=300;质量为m、带电量为+q(q>0)的粒子2在纸面内以速度V2=$\sqrt{3}$V0也从O点射入磁场,其射入方向与MN的夹角β=60°.已知粒子1和2同时分别到达磁场边界的A、B两点(图中未画出),不计粒子的重力及它们间的相互作用.
如图所示.直线MN上方垂直纸面向里的、磁感应强度为B的匀强磁场,质量为m、带电量为-q(q>0)的粒子1在纸面内以速度V1=V0从O点射入磁场,其射入方向与MN的夹角α=300;质量为m、带电量为+q(q>0)的粒子2在纸面内以速度V2=$\sqrt{3}$V0也从O点射入磁场,其射入方向与MN的夹角β=60°.已知粒子1和2同时分别到达磁场边界的A、B两点(图中未画出),不计粒子的重力及它们间的相互作用.(1)求两个粒子在磁场边界上的穿出点A、B之间的距离.
(2)求两个粒子进入磁场的时间间隔△t.
(3)若MN下方有平行于纸面的匀强电场,且两粒子在电场中相遇,其中粒子1做直线运动.求该电场的电场强度.
分析 (1)两个粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,列式可求得轨迹半径.由几何关系求出轨迹对应的圆心角,再运用几何知识求解A、B之间的距离.
(2)粒子圆周运动的周期 T=$\frac{2πr}{v}$,根据轨迹对应的圆心角求出各自运动的时间,即可得到时间间隔△t.
(3)电场强度的方向应与粒子1穿出磁场的方向平行.可能有两种:
a、若场强的方向与MN成30°角向上偏右,则粒子1做匀加速直线运动,粒子2做类平抛运动;
b、若场强的方向与MN成30°角向下偏左,则粒子1做匀减速直线运动,粒子2做类平抛运动.由牛顿第二定律和运动学公式结合求解.
解答 解:(1)粒子在磁场中做匀速圆周运动,由牛顿运动定律得 Bqv=m$\frac{{v}^{2}}{r}$
解得 r1=$\frac{m{v}_{0}}{qB}$和r2=$\frac{\sqrt{3}m{v}_{0}}{qB}$
由几何关系可知:
粒子1圆周运动的圆弧所对的圆心角为 θ1=$\frac{5}{3}$π
所以射入点O与离开磁场的位置A间的距离 OA=2r1sin$\frac{2π-{θ}_{1}}{2}$
粒子2圆周运动的圆弧所对的圆心角为 θ1=$\frac{4}{3}$π
所以射入点O与离开磁场的位置B间的距离 OB=2r2sin$\frac{2π-{θ}_{2}}{2}$
故穿出点A、B之间的距离 d=OA+OB=$\frac{4m{v}_{0}}{qB}$
(2)粒子圆周运动的周期 T=$\frac{2πr}{v}$
粒子1在磁场中运动的时间 t1=$\frac{{θ}_{1}}{2π}$T
粒子2在磁场中运动的时间 t2=$\frac{{θ}_{2}}{2π}$T
进入磁场的时间间隔△t=t1-t2=$\frac{πm}{3qB}$
(3)由题意电场强度的方向应与粒子1穿出磁场的方向平行.
a、若场强的方向与MN成30°角向上偏右,则粒子1做匀加速直线运动,粒子2做类平抛运动
对粒子1、2 由运动定律得 Eq=ma
在粒子1的运动所在直线上,
对粒子1和2由位移公式得 ABcos30°=v1t+$\frac{1}{2}$at2+$\frac{1}{2}$at2
在与粒子1的运动垂直的方向上,
对粒子2由位移公式得 ABsin30°=v2t
解得 E=$\sqrt{3}$B v0
b、若场强的方向与MN成30°角向下偏左,则粒子1做匀减速直线运动,粒子2做类平抛运动
对粒子1、2 由运动定律得 Eq=ma
在粒子1的运动所在直线上,
对粒子1和2由位移公式得 AB cos30°=v1t-$\frac{1}{2}$at2-$\frac{1}{2}$at2
在与粒子1的运动垂直的方向上,
对粒子2由位移公式得 AB sin30°=v2t
解得 E=-$\sqrt{3}$Bv0
假设不成立.
综上所述:场强的大小为$\sqrt{3}$B v0,方向为与MN成30°角向上偏右.
答:
(1)两个粒子在磁场边界上的穿出点A、B之间的距离为$\frac{4m{v}_{0}}{qB}$.
(2)两个粒子进入磁场的时间间隔△t为$\frac{πm}{3qB}$.
(3)场强的大小为$\sqrt{3}$B v0,方向为与MN成30°角向上偏右.
点评 该题中带电粒子在磁场中运动的半径与周期的公式的推导与应用,要熟练掌握,由轨迹的圆心角求时间是常用方法,基本公式是t=$\frac{θ}{2π}$T,θ是轨迹对应的圆心角.

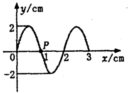 一列简谐横波在t=0时的波形如图所示,当t=0.25s时图中P点第一次到达波峰的位置,当t=0.75s时有( )
一列简谐横波在t=0时的波形如图所示,当t=0.25s时图中P点第一次到达波峰的位置,当t=0.75s时有( )| A. | P点的速度为0 | B. | P点的位移为-2cm | ||
| C. | 波的周期为1s | D. | 这列波的波速为6cm/s |
| A. | 整个回路在磁场中运动 | |
| B. | 回路所在处的磁场发生变化 | |
| C. | 穿过回路的磁通量发生变化 | |
| D. | 回路中的一部分导体做切割磁感线运动 |
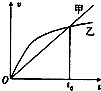 甲、乙两物体从离地面相同高度同时由静止开始下落,将释放时刻作为t=0时刻,两物体的v-t图象如图所示,则下列判断正确的是( )
甲、乙两物体从离地面相同高度同时由静止开始下落,将释放时刻作为t=0时刻,两物体的v-t图象如图所示,则下列判断正确的是( )| A. | t0时刻之前,甲物体的加速度一直大于乙物体的加速度 | |
| B. | 0-t0时间内,甲物体中间时刻速度大于乙物体平均速度 | |
| C. | t0时刻甲、乙两物体到达同一高度 | |
| D. | t0时刻之前甲离地高度总大于乙物体离地的高度 |
| A. | 密闭在容器中的气体,在某一时刻向各个方向运动的气体分子数目一定相等 | |
| B. | 大量气体分子的速率有大有小,但是按“中间多,两头少”的规律分布 | |
| C. | 气体压强的大小跟气体分子的平均动能、分子的密集程度这两个因素有关 | |
| D. | 一定质量的理想气体,温度不变,体积减小时,气体的内能一定增大 |
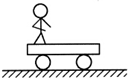 如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )
如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )| A. | 人和车组成的系统水平方向动量不守恒 | |
| B. | 人和车组成的系统机械能守恒 | |
| C. | 人和车的速度方向相同 | |
| D. | 人停止行走时,人和车的速度一定均为零 |
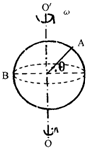 花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )| A. | B点的角速度大于A点角速度 | B. | A、B两点线速度大小相等 | ||
| C. | A、B两点的周期相等 | D. | A、B两点向心加速度大小相等 |
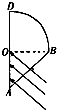 一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长.
一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长. 有一柱状透明体,长度为L,其折射率为n1.
有一柱状透明体,长度为L,其折射率为n1.