题目内容
3.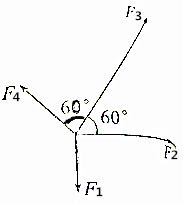 如图所示,同一平面上的四个共点力大小分别是F1=2N,F2=F4=4N,F3=10N方向如图所示,求其合力.
如图所示,同一平面上的四个共点力大小分别是F1=2N,F2=F4=4N,F3=10N方向如图所示,求其合力.
分析 建立坐标系:以四个力的作用点为原点,以F2方向为x轴正方向,以F1方向的反方向为y轴方向,将F1、F3、F4分解到两个坐标轴上,分别求出x轴和y轴上的合力,再求解四个力的合力的大小和方向.
解答 解:由题图中可知,F1与F2垂直,以F1方向为x轴正方向,以F2方向为y轴方向,将F1、F3、F4分解到两个坐标轴上,如图
可知;F3和F4与y轴之间的夹角都是30°
建立直角坐标系 Fx=F2+F3x+F4x=4+10×sin30°+4×sin120°=7N;
Fy=F1+F3y+F4y=-2+10×cos30°+4×cos30°=(7$\sqrt{3}$-2)N;
四个力的合力F=$\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=12.3$N
合力的方向:tanθ=$\frac{{F}_{y}}{{F}_{x}}=\frac{7\sqrt{3}-2}{7}≈1.44$,
即F与F2的方向之间的夹角为arctan1.44.
答:四个力的合力大小为12.3N,方向与F2的方向之间的夹角为arctan1.44.
点评 正交分解法是求解合力的一种方法,首先要建立坐标系,先正交分解,再求解合力.

练习册系列答案
相关题目
11.如图所示.已知电源电动势E=2V,电源内阻r=0.5Ω,小灯泡电阻R0=2Ω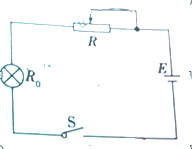 ,滑动变阻器R最大阻值为10Ω.当开关闭合后,调节滑动变阻器,设灯泡电阻不随温度变化而变化,则.
,滑动变阻器R最大阻值为10Ω.当开关闭合后,调节滑动变阻器,设灯泡电阻不随温度变化而变化,则.
 ,滑动变阻器R最大阻值为10Ω.当开关闭合后,调节滑动变阻器,设灯泡电阻不随温度变化而变化,则.
,滑动变阻器R最大阻值为10Ω.当开关闭合后,调节滑动变阻器,设灯泡电阻不随温度变化而变化,则.| A. | 当滑动变阻器阻值调至0.5Ω时,电源输出功率最大 | |
| B. | 当滑动变阻器阻值凋至1.5Ω时,灯泡最亮 | |
| C. | 当滑动变阻器阻值逐渐减小时,电源输出功率逐渐增大 | |
| D. | 当滑动变阻器阻值凋至2.5Ω时,滑动变阻器的电功率最大. |
15. 如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )
如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )
 如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )
如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )| A. | 恰好可以到达开始的释放点 | B. | 恰好可以到达P点 | ||
| C. | 到达P后,继续上升一段时间 | D. | 不能到达P点 |
14.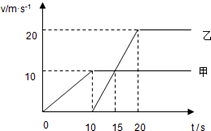 甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动,它们的 v-t图象如图所示.下列判断正确的是( )
甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动,它们的 v-t图象如图所示.下列判断正确的是( )
 甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动,它们的 v-t图象如图所示.下列判断正确的是( )
甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动,它们的 v-t图象如图所示.下列判断正确的是( )| A. | 乙车启动时,甲车在其前方100m处 | |
| B. | 运动过程中,乙车落后甲车的最大距离为75m | |
| C. | 乙车启动10s后正好追上甲车 | |
| D. | 乙车超过甲车后,两车不会再相遇 |
 在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.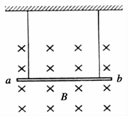 用两根绝缘的轻质细绳,将长为0.6m、质量为0.06kg的均匀金属杆ab,水平悬挂在磁感应强度大小为2T、方向如图所示的磁场中.问:要使细绳的拉力恰好为零,应在ab中通入多大的电流?方向如何?(取g=10m/s2).
用两根绝缘的轻质细绳,将长为0.6m、质量为0.06kg的均匀金属杆ab,水平悬挂在磁感应强度大小为2T、方向如图所示的磁场中.问:要使细绳的拉力恰好为零,应在ab中通入多大的电流?方向如何?(取g=10m/s2).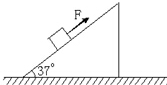 如图所示,物重G=100N,它与倾角为37°的斜面间的动摩擦因数μ=0.2,使物体沿斜面做加速度大小为2m/s2的匀加速运动,作用在物体上的一平行于斜面向上的外力F要多大?(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,物重G=100N,它与倾角为37°的斜面间的动摩擦因数μ=0.2,使物体沿斜面做加速度大小为2m/s2的匀加速运动,作用在物体上的一平行于斜面向上的外力F要多大?(sin37°=0.6,cos37°=0.8,g=10m/s2)