题目内容
15. 如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )
如图,一半径为R,粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平,一质点自P点上方高度R处由静止开始释放,恰好从P点进入轨道,发现质点滑出Q点后能上升$\frac{R}{2}$,则质点再次返回PNQ轨道后( )| A. | 恰好可以到达开始的释放点 | B. | 恰好可以到达P点 | ||
| C. | 到达P后,继续上升一段时间 | D. | 不能到达P点 |
分析 对质点开始下落到Q点的过程运用动能定理求出克服摩擦力做功的大小.抓住质点返回时摩擦力减小,相同路程克服摩擦力做功减小,根据动能定理判断能否返回P点.
解答 解:质点从静止下落到运动到Q点上方的过程,设克服摩擦力做功为W.
根据动能定理得:mg(R-$\frac{R}{2}$)-W=0,得 W=$\frac{1}{2}$mgR
假设质点能返回到P点,到达P点的速度为v,此过程克服摩擦力做功为W′.
由动能定理得:mg$\frac{R}{2}$-W′=$\frac{1}{2}m{v}^{2}$
由于质点从Q返回到P点的过程与从P运动到Q的过程相比,经过同一点的速度小,向心力小,则轨道对质点的支持力小,摩擦力也小,所以有:W′<W.
可得,v>0,所以质点到达P后,继续上升一段时间,故ABD错误,C正确.
故选:C
点评 本题考查了动能定理和牛顿第二定律的综合运用,根据向心力知识来回的速度关系是关键.注意在QP段克服摩擦力做功小于在PQ段克服摩擦力做功.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
10.两个同学在做引体向上时,甲同学两手距离与肩同宽,乙同学两手距离大于肩宽,则下列说法正确的是( )
| A. | 甲同学更省力 | |
| B. | 乙同学更省力 | |
| C. | 两个同学一样费力 | |
| D. | 若两手挨在一起,比甲、乙同学都省力 |
1.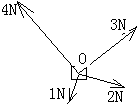 如图所示,一物体受到1N、2N、3N、4N四个力作用而处于平衡,沿3N力的方向作匀速直线运动,现保持1N、3N、4N三个力的方向和大小不变,而将2N的力绕O点旋转60°,此时作用在物体上的合力大小为( )
如图所示,一物体受到1N、2N、3N、4N四个力作用而处于平衡,沿3N力的方向作匀速直线运动,现保持1N、3N、4N三个力的方向和大小不变,而将2N的力绕O点旋转60°,此时作用在物体上的合力大小为( )
 如图所示,一物体受到1N、2N、3N、4N四个力作用而处于平衡,沿3N力的方向作匀速直线运动,现保持1N、3N、4N三个力的方向和大小不变,而将2N的力绕O点旋转60°,此时作用在物体上的合力大小为( )
如图所示,一物体受到1N、2N、3N、4N四个力作用而处于平衡,沿3N力的方向作匀速直线运动,现保持1N、3N、4N三个力的方向和大小不变,而将2N的力绕O点旋转60°,此时作用在物体上的合力大小为( )| A. | 2N | B. | 2$\sqrt{2}$N | C. | 3N | D. | 3$\sqrt{3}$N |
6.两个物体从同一地点先后自由下落,甲比乙先下落2秒,下面说法正确的是( )
| A. | 甲相对乙的运动是匀速直线运动 | |
| B. | 两物体落地之前总保持20m的距离不变 | |
| C. | 两物体间的距离越来越大 | |
| D. | 两物体间的距离越来越小 |
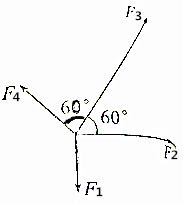 如图所示,同一平面上的四个共点力大小分别是F1=2N,F2=F4=4N,F3=10N方向如图所示,求其合力.
如图所示,同一平面上的四个共点力大小分别是F1=2N,F2=F4=4N,F3=10N方向如图所示,求其合力. 如图所示为质谱仪的示意图.速度选择器部分的匀强电场场强E,匀强磁场的磁感应强度为B1;偏转分离器的磁感应强度为B2.一质量为m,电荷量为+q的带电微粒进入速度选择器.不计带电微粒的重力.求:
如图所示为质谱仪的示意图.速度选择器部分的匀强电场场强E,匀强磁场的磁感应强度为B1;偏转分离器的磁感应强度为B2.一质量为m,电荷量为+q的带电微粒进入速度选择器.不计带电微粒的重力.求: