题目内容
1.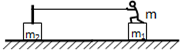 质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )
质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )| A. | FS2 | B. | F(S1+S2) | ||
| C. | m2v22 | D. | m2v22+(m+m1)v12 |
分析 欲求人做的功不外乎两个方法:1、根据做功的定义由恒力做功公式求出;2、利用功能关系或动能定理求出增加的能量即为功的多少.
解答 解:根据功能关系知道:人做的功都转化成了系统的能量,即m1、m2和人的动能,则得人做功为 W=m2v22+(m+m1)v12.
根据恒力做功的计算方法绳子上的力也为F,由恒力做功公式W=FS得:W=F(S1+S2),故BD正确.
故选:BD
点评 这是一道全面考查恒力做功计算的题目,定义法求功和间接计算能量是等效的,虽然答案的形式不同但功能相当.

练习册系列答案
相关题目
12.一个物体在距地面高度为地球半径的2倍时所受地球的引力为F,则在地球表面所受地球引力为( )
| A. | 2F | B. | 3F | C. | 4F | D. | 9F |
9.我国自行研制的可控热核反应实验装置“超导托卡马克”(英文名称:EAST,俗称“人造太阳”).设可控热核试验反应前氘(H)的质量为m1,氚核(H)的质量为m2,反应后氦核(He)的质量为m3,中子(n)的质量为m4,光速为c.下列说法正确的是( )
| A. | 这种装置发生的核反应方程式是H+H→He+n | |
| B. | 由核反应过程质量守恒可知m1+m2=m3+m4 | |
| C. | 核反应放出的能量等于(m1+m2+m3-m4 )c2 | |
| D. | 这种装置与我国大亚湾核电站所使用核装置的核反应原理相同 |
16.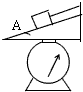 如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )
如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )
 如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )
如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )| A. | 增加 | B. | 减少 | C. | 不变 | D. | 无法判断 |
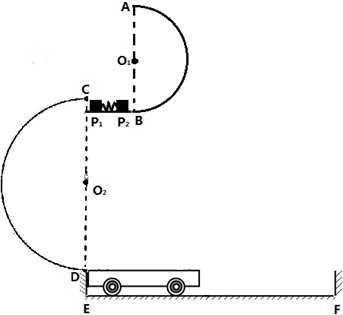
6. 如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
 如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )| A. | 重力、支持力、沿切线的摩擦力 | B. | 重力、支持力、向心力、摩擦力 | ||
| C. | 重力、支持力、指向圆心的摩擦力 | D. | 重力、支持力 |
13.关于功和能的关系,下列说法中正确的是( )
| A. | 功是能量变化的量度 | |
| B. | 路径不同,重力所做的功一定不同 | |
| C. | 弹力做正功,弹性势能一定增加 | |
| D. | 合外力对物体做正功,物体的动能一定增加 |
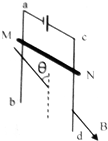
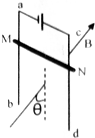
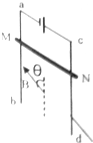
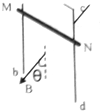
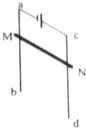 如图所示,电阻为R的金属棒MN水平靠在光滑的竖直导轨外侧,与导轨接触良好,导轨的上端与电源连接,导轨电阻不计,整个装置置于方向与导轨平面成θ角且与金属棒MN垂直的匀强磁场中,图中所加磁场的方向能使MN静止的是( )
如图所示,电阻为R的金属棒MN水平靠在光滑的竖直导轨外侧,与导轨接触良好,导轨的上端与电源连接,导轨电阻不计,整个装置置于方向与导轨平面成θ角且与金属棒MN垂直的匀强磁场中,图中所加磁场的方向能使MN静止的是( )