题目内容
16. 如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )
如图所示,重4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态,倾角为30°的斜面被固定在测力计上,物块与斜面间无摩擦,装置稳定后,当细线被烧断物块正在下滑时与静止时比较,测力计的示数( )| A. | 增加 | B. | 减少 | C. | 不变 | D. | 无法判断 |
分析 本题中原来物块和斜面体处于静止状态,故测力计的读数等于物块和斜面体的总重量,剪短细线后,沿斜面小球加速下滑,处于失重状态,对小球和斜面体整体运用牛顿第二定律列式求解.
解答 解:对物块和斜面体整体受力分析,受总重力和支持力,平衡时,有:
N-(M+m)g=0…①
加速下滑时,再次对物块和斜面体整体受力分析,受总重力、支持力和静摩擦力,根据牛顿第二定律,有
竖直方向:(M+m)g-N′=masin30°…②
水平方向:f=macos30°…③
对物块受力分析,受重力和支持力,根据牛顿第二定律,有
mgsin30°=ma…④
有由①②③④得到:
N-N′=masin30°=mg(sin30°)2=0.4×10×0.25=1N
故说明测力计的示数减小了1N;
故选:B.
点评 本题关键是对物块、物块和斜面体整体多次受力分析,然后根据牛顿第二定律、共点力平衡条件列式求解;要注意整体法对于有相对运动的物体系统同样适用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.关于近代物理,下列说法正确的是( )
| A. | 单个氢原子从n=4向较低能级跃迁时,最多可以向外辐射6种不同频率光线 | |
| B. | 核聚变反应方程 ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H-→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n中,${\;}_{0}^{1}$n表示质子 | |
| C. | 从金属表面逸出的光电子的最大初动能与照射光的频率成正比 | |
| D. | 在核反应方程 ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{54}^{140}$Xe+${\;}_{38}^{94}$Sr+d${\;}_{0}^{1}$n中,d的大小是2 |
7. 如图所示,在高为1.5m的光滑平台上有-个质量为2kg的小球被一细线栓在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,取g=10m/s2,则弹簧被压缩时具有的弹性势能为( )
如图所示,在高为1.5m的光滑平台上有-个质量为2kg的小球被一细线栓在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,取g=10m/s2,则弹簧被压缩时具有的弹性势能为( )
 如图所示,在高为1.5m的光滑平台上有-个质量为2kg的小球被一细线栓在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,取g=10m/s2,则弹簧被压缩时具有的弹性势能为( )
如图所示,在高为1.5m的光滑平台上有-个质量为2kg的小球被一细线栓在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,取g=10m/s2,则弹簧被压缩时具有的弹性势能为( )| A. | 10J | B. | 15J | C. | 20J | D. | 25J |
11.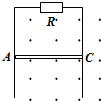 如图所示,回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体棒AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的是( )
如图所示,回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体棒AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的是( )
 如图所示,回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体棒AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的是( )
如图所示,回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体棒AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的是( )| A. | 导体下落过程中,机械能守恒 | |
| B. | 导体加速下落过程中,导体减少的重力势能全部转化为电阻产生的热量 | |
| C. | 导体加速下落过程中,导体减少的重力势能转化为导体增加的动能 | |
| D. | 导体达到稳定速度后的下落过程中,导体减少的重力势能全部转化为回路中增加的内能 |
1. 质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )
质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )
 质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )
质量为m1、m2的两物体,静止在光滑的水平面上,质量为m的人站在m1上用恒力F拉绳子,经过一段时间后,两物体的速度大小分别为v1和v2,位移分别为S1和S2,如图所示,则这段时间内此人所做的功的大小等于( )| A. | FS2 | B. | F(S1+S2) | ||
| C. | $\frac{1}{2}$m2v22 | D. | $\frac{1}{2}$m2v22+$\frac{1}{2}$(m+m1)v12 |
8. 如图所示,物体从高度为h的光滑固定斜面顶端A点开始下滑,在滑行到斜面底端B点时,速度的大小为(不计空气阻力)( )
如图所示,物体从高度为h的光滑固定斜面顶端A点开始下滑,在滑行到斜面底端B点时,速度的大小为(不计空气阻力)( )
 如图所示,物体从高度为h的光滑固定斜面顶端A点开始下滑,在滑行到斜面底端B点时,速度的大小为(不计空气阻力)( )
如图所示,物体从高度为h的光滑固定斜面顶端A点开始下滑,在滑行到斜面底端B点时,速度的大小为(不计空气阻力)( )| A. | $\frac{1}{2}$gh | B. | gh | C. | 2gh | D. | $\sqrt{2gh}$ |
5.下列关于地球同步卫星说法中正确的是( )
| A. | 地球同步卫星只能在地球赤道上空同一条轨道中运动 | |
| B. | 地球同步卫星的周期大于地球自转的周期 | |
| C. | 所有地球同步卫星的速率都是一个确定值 | |
| D. | 所有地球同步卫星的向心力都相同 |



