题目内容
13. 如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )
如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )| A. | A、B的运动时间相同 | B. | A、B沿x轴方向的位移相同 | ||
| C. | A的轨迹是抛物线,B的轨迹是椭圆 | D. | A、B落地点的速率相同 |
分析 A在竖直平面内做平抛运动,B在光滑的斜面上做类平抛运动,将运动进行分解,结合合运动与分运动的关系求解.根据动能定理,重力做功等于动能的增量,求解末速度.
解答 解:A、A在竖直平面内做平抛运动,竖直方向是自由落体运动,B在斜面上运动,受到重力和支持力,沿斜面向下是匀加速运动,加速度是gsinθ,所以B运动的时间长,AB的轨迹都是抛物线,故AC错误.
B、A、B在水平方向都是匀速运动,由于水平方向的初速度相同,B运动时间长,所以B落地点P2在x轴上的投影要比P1长,故B错误.
D、根据动能定理得A、B运动过程中:mgh=$\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{v}^{2}$
解得:v=$\sqrt{{v}^{2}+2gh}$,故A、B落地时速率一样大. 故D正确.
故选:D.
点评 本题关键是先确定B参与沿与水平方向和沿斜面方向的运动,然后根据合运动与分运动的等效性,由平行四边形定则求解.

练习册系列答案
相关题目
8.雨滴从很高的地方竖直下落,若空气阻力和其速度成正比,则雨滴的运动情况可能是( )
| A. | 开始时重力大于空气阻力,后来重力小于空气阻力 | |
| B. | 先匀加速后匀速,直到落地 | |
| C. | 加速度越来越小,最后为零 | |
| D. | 先加速后减速,最后匀速 |
4.一个电阻接到某电路后,消耗的功率为220W,通过3C的电荷量时,有330J的电能转化为内能,则下列说法正确的是( )
| A. | 电阻所加电压为220V | B. | 通过电阻的电流为2A | ||
| C. | 电阻通电时间为2s | D. | 这个电阻的阻值为110Ω |
8.关于点电荷所形成的电场,下列说法正确的是( )
| A. | 以点电荷为球心的某球面上,各点的场强不相同 | |
| B. | 以点电荷为球心的某球面上,各点的电势不相同 | |
| C. | 沿着负点电荷形成电场的电场线方向,场强越来越小 | |
| D. | 沿着正点电荷形成电场的电场线方向,电势越来越高 |
18.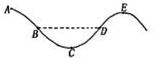 在竖直平面内,一根光滑金属杆弯成如图所示形状,B、D两点等高,将一个光滑小环套在该金属杆上,并从A点以某一初速度沿杆向右运动.运动过程中( )
在竖直平面内,一根光滑金属杆弯成如图所示形状,B、D两点等高,将一个光滑小环套在该金属杆上,并从A点以某一初速度沿杆向右运动.运动过程中( )
 在竖直平面内,一根光滑金属杆弯成如图所示形状,B、D两点等高,将一个光滑小环套在该金属杆上,并从A点以某一初速度沿杆向右运动.运动过程中( )
在竖直平面内,一根光滑金属杆弯成如图所示形状,B、D两点等高,将一个光滑小环套在该金属杆上,并从A点以某一初速度沿杆向右运动.运动过程中( )| A. | 小环经过A点时的机械能最大 | |
| B. | 小环经过B点和E点的动能相等 | |
| C. | 小环经过C点的动能最大 | |
| D. | 小环从A点运动到D点的过程中,重力势能的减少量等于动能的减少量 |
3.甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v-t图象如图所示,则( )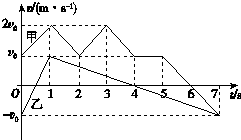

| A. | 在t=0到t=1 s内甲、乙之间的距离先增大后减小 | |
| B. | 甲、乙在t=7 s时到达同一位置 | |
| C. | 甲在t=0到t=4 s之间做往复运动 | |
| D. | 甲、乙在t=6 s时的加速度方向相同 |
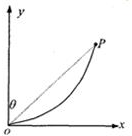 一质点在xOy平面内的运动轨迹如图所示,质点从坐标原点O开始运动,运动过程中受到二恒力F1、F2作用,最后到达P点.已知恒力F1沿x轴方向,恒力F2沿y轴方向.O、P两点连线与y轴的夹角为θ,则在这一运动过程中,恒力F1的方向为x轴的正方向(填“正”或“负”);恒力F2做的功为正功.
一质点在xOy平面内的运动轨迹如图所示,质点从坐标原点O开始运动,运动过程中受到二恒力F1、F2作用,最后到达P点.已知恒力F1沿x轴方向,恒力F2沿y轴方向.O、P两点连线与y轴的夹角为θ,则在这一运动过程中,恒力F1的方向为x轴的正方向(填“正”或“负”);恒力F2做的功为正功.