题目内容
2.一回旋加速器,在外磁场一定时,可把质子(${\;}_{1}^{1}$H)加速到v,使它获得动能为Ek,则:能把α粒子(${\;}_{2}^{4}$He)加速到的最大速度为$\frac{1}{2}v$,能使α粒子获得的最大动能为Ek .分析 交流电的周期和粒子做圆周运动的周期相等,粒子在圆周运动的过程中一次一次地经过D形盒缝隙,两盒间的电势差一次一次地反向,粒子就会被一次一次地加速.由牛顿第二定律推导出最大速度的表达式进行讨论即可.
解答 解:根据qvB=m$\frac{{v}^{2}}{R}$ 得粒子出D形盒时的速度为:vm=$\frac{qBR}{m}$;
可把质子加速到v,故有:v=$\frac{eBR}{m}$;
当加速α粒子时,有:v′=$\frac{eBR}{2m}$=$\frac{v}{2}$;
能使α粒子获得的最大动能为Ek′=$\frac{1}{2}×4mv{′}^{2}$=Ek
故答案为:$\frac{1}{2}v$,Ek
点评 回旋加速器应用了带电粒子在电场中加速、在磁场中偏转(匀速圆周运动)的原理.最大速度与电压无关.

练习册系列答案
相关题目
13. 如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )
如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )
 如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )
如图所示,A、B两质点以相同的水平速度v抛出,A在竖直平面内运动,落地点在P1;B在光滑的斜面上运动,落地点在P2,P1、P2在同一水平面上.不计空气阻力,则下列说法中正确的是( )| A. | A、B的运动时间相同 | B. | A、B沿x轴方向的位移相同 | ||
| C. | A的轨迹是抛物线,B的轨迹是椭圆 | D. | A、B落地点的速率相同 |
10.以下说法正确的是( )
| A. | 法拉第发现了电场中电场线的存在 | |
| B. | 库仑提出了库仑定律,并最早用实验测得静电力常量 | |
| C. | 牛顿发现了万有引力定律,并最先计算出了地球的质量 | |
| D. | 带电体的电荷量只能是元电荷的整数倍 |
17.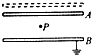 如图所示,水平放置的两平行的金属板A、B带电量均异种电荷,A板带负电荷,B板接地,P是A、B两板中间的一点,若将A板向上平移到虚线位置.则P点的电场强度E和电势φ的变化情况是( )
如图所示,水平放置的两平行的金属板A、B带电量均异种电荷,A板带负电荷,B板接地,P是A、B两板中间的一点,若将A板向上平移到虚线位置.则P点的电场强度E和电势φ的变化情况是( )
 如图所示,水平放置的两平行的金属板A、B带电量均异种电荷,A板带负电荷,B板接地,P是A、B两板中间的一点,若将A板向上平移到虚线位置.则P点的电场强度E和电势φ的变化情况是( )
如图所示,水平放置的两平行的金属板A、B带电量均异种电荷,A板带负电荷,B板接地,P是A、B两板中间的一点,若将A板向上平移到虚线位置.则P点的电场强度E和电势φ的变化情况是( )| A. | E不变,φ不变 | B. | E变小,φ变低 | C. | E变大,φ变高 | D. | E变大,φ变低 |
7. 材料:淮安有轨电车一期工程线路西起市体育馆,沿交通路至大运河广场北侧,经和平路至水渡口广场,向南沿翔宇大道、楚州大道至淮安区商贸城,全长20.3公里,共设车站23个.工程估算投资约32亿元,若全程采用地面供电方式将达37亿元左右.2014年2月19日8时,淮安市有轨电车工程全面开工,2015年初将实现首列车进场调试.到时淮安的市民将有机会乘坐轨电车,最高时速可为80km/h,列车长度34800mm,车辆高度为3500mm.
材料:淮安有轨电车一期工程线路西起市体育馆,沿交通路至大运河广场北侧,经和平路至水渡口广场,向南沿翔宇大道、楚州大道至淮安区商贸城,全长20.3公里,共设车站23个.工程估算投资约32亿元,若全程采用地面供电方式将达37亿元左右.2014年2月19日8时,淮安市有轨电车工程全面开工,2015年初将实现首列车进场调试.到时淮安的市民将有机会乘坐轨电车,最高时速可为80km/h,列车长度34800mm,车辆高度为3500mm.
结合以上材料,下列情况可以把有轨电车看成质点的是( )
 材料:淮安有轨电车一期工程线路西起市体育馆,沿交通路至大运河广场北侧,经和平路至水渡口广场,向南沿翔宇大道、楚州大道至淮安区商贸城,全长20.3公里,共设车站23个.工程估算投资约32亿元,若全程采用地面供电方式将达37亿元左右.2014年2月19日8时,淮安市有轨电车工程全面开工,2015年初将实现首列车进场调试.到时淮安的市民将有机会乘坐轨电车,最高时速可为80km/h,列车长度34800mm,车辆高度为3500mm.
材料:淮安有轨电车一期工程线路西起市体育馆,沿交通路至大运河广场北侧,经和平路至水渡口广场,向南沿翔宇大道、楚州大道至淮安区商贸城,全长20.3公里,共设车站23个.工程估算投资约32亿元,若全程采用地面供电方式将达37亿元左右.2014年2月19日8时,淮安市有轨电车工程全面开工,2015年初将实现首列车进场调试.到时淮安的市民将有机会乘坐轨电车,最高时速可为80km/h,列车长度34800mm,车辆高度为3500mm.结合以上材料,下列情况可以把有轨电车看成质点的是( )
| A. | 研究有轨电车的车轮在轨道上如何转动 | |
| B. | 研究有轨电车转弯 | |
| C. | 估算市体育馆至淮安区商贸城所需时间 | |
| D. | 估算有轨电车过红绿灯所需时间 |
11.小球A沿高为h、倾角为θ的光滑斜面以初速度v0从顶端滑到底端.相同的小球B以同样大小的初速度v0从同一高度竖直上抛,则( )
| A. | 两物体落地时速率相同 | |
| B. | 从开始运动至落地过程中,重力对B球做功多 | |
| C. | 两物体落地时,重力的瞬时功率相同 | |
| D. | 从开始运动至落地过程中,重力对它们做功的平均功率相同 |
 甲乙两车同时从同一地点出发,甲以6m/s的速度作匀速直线运动,乙以初速度为零加速度为1m/s2的加速度启动8秒后做匀速运动和甲同向作直线运动,求:
甲乙两车同时从同一地点出发,甲以6m/s的速度作匀速直线运动,乙以初速度为零加速度为1m/s2的加速度启动8秒后做匀速运动和甲同向作直线运动,求: