题目内容
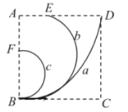
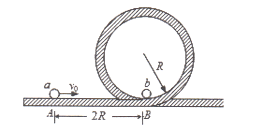
【题目】过山车是游乐场中常见的设施之一。下图是过山车模型的一部分，它由足够长的水平轨道和半径为R的竖直光滑圆形轨道组成，B点是圆形轨道的最低点。一质量为2m的小球a，由距B点2R的A点以初速度vo（vo未知）水平向右运动，在B点与质量为m的小球b发生弹性正碰，碰后a未脱离轨道。已知a、b与水平轨道的动摩擦因数均为μ，重力加速度为g。
(1)若碰后b恰能到达轨道上与圆心等高处，求a的初速度vo；
(2)若碰后b恰能越过轨道的最高点，求最终a、b两球的水平距离x。
【答案】（1）
（2）
【解析】
（1）设小球a在B点碰撞前的速度为v，由动能定理得：
a、b球碰撞，设碰撞后a、b球的速度分别为
，
，由动量守恒和机械能守恒定律得
碰撞后b球恰能到圆心等高处，由机械能守恒得：
联立得：
（2）碰后b恰能越过轨道最高点的速度为
，由牛顿第二定律得：
B碰后到最高点的过程，由机械能守恒得
B球经轨道回到B点右侧受阻力，设经
而停止，由动能定理得
解得：
碰后a球的速度
A球滑上轨道后，将返回水平轨道向左运动，设经
而停止，由动能定理得
得：
则最终ab两球得水平距离为：
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
