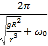Question

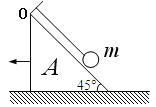
【题目】如图,拖拉机前轮与后轮的半径之比为1:2,A和B是前轮和后轮边缘上的点,若车行进时轮没有打滑,则

A. 两轮转动的周期相等 B. 前轮和后轮的角速度之比为1:2

C. A点和B点的线速度大小之比为1:2 D. A点和B点的向心加速度大小之比为2:1

Answer 1

【答案】D

【解析】

传动装置，在传动过程中不打滑，则有：共轴的角速度是相同的；同一传动装置接触边缘的线速度大小是相等的．所以当角速度一定时，线速度与半径成正比；当线速度大小一定时，角速度与半径成反比．因此根据题目条件可知线速度及角速度关系即可求解．

根据v=ωr和vA=vB，可知A、B两点的角速度之比为2：1；故B错误。据和前轮与后轮的角速度之比2：1，求得两轮的转动周期为1：2，故A错误。轮A、B分别为同一传动装置前轮和后轮边缘上的一点，所以vA=vB，故C错误。由a=ωv，可知A与B点的向心加速度之比为2：1，故D正确。故选D。