题目内容
从地面上发射质量为m的导弹,导弹的喷气发动机可产生恒定的推力,推力大小F= mg,使导弹沿与水平方向成α=30°角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间
mg,使导弹沿与水平方向成α=30°角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间 ,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).
,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).
解:开始时导弹做匀加速直线运动,受力分析如下图甲所示:
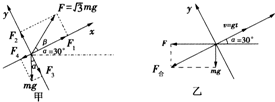
y方向: mgsinβ-mgcos 30°=0 所以β=30°
mgsinβ-mgcos 30°=0 所以β=30°
x方向: mgcosβ-mgsin 30°=ma1 所以a1=g
mgcosβ-mgsin 30°=ma1 所以a1=g
经过时间t,导弹的速度v=a1t=gt,斜向上运动的距离s1= .
.
此时将推力逆时针旋转120°,推力F将水平向左,导弹的受力分析如图乙所示,
显然F合=-2mg=ma2,所以a2=-2g,再经过时间 ,导弹速度正好减为零,
,导弹速度正好减为零,
同时斜向上运动的距离s2=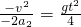
此时关闭发动机,导弹将从静止自由下落,故导弹落地点距发射点的距离为
L=(s1+s2) cos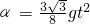
再由(s1+s2) sinα=
得t自=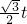 .
.
答:再经过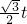 时间导弹落回地面,落地点离发射点
时间导弹落回地面,落地点离发射点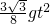 .
.
分析:作出导弹匀加速直线运动的受力分析图,根据牛顿第二定律求出加速度,结合运动学公式求出t后的速度和位移,将推力的方向逆时针转动120°,根据牛顿第二定律再次求出导弹的加速度,判断出导弹的运动情况,结合运动学公式求出导弹经过时间 的速度和位移,关闭发动机后,根据受力判断出物体的运动情况,结合运动学公式求出导弹落地的时间和落地点离发射点的位移.
的速度和位移,关闭发动机后,根据受力判断出物体的运动情况,结合运动学公式求出导弹落地的时间和落地点离发射点的位移.
点评:解决本题的关键理清导弹在整个过程中的运动情况,结合牛顿第二定律和运动学公式进行求解.

y方向:
 mgsinβ-mgcos 30°=0 所以β=30°
mgsinβ-mgcos 30°=0 所以β=30°x方向:
 mgcosβ-mgsin 30°=ma1 所以a1=g
mgcosβ-mgsin 30°=ma1 所以a1=g经过时间t,导弹的速度v=a1t=gt,斜向上运动的距离s1=
 .
.此时将推力逆时针旋转120°,推力F将水平向左,导弹的受力分析如图乙所示,
显然F合=-2mg=ma2,所以a2=-2g,再经过时间
 ,导弹速度正好减为零,
,导弹速度正好减为零,同时斜向上运动的距离s2=
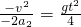
此时关闭发动机,导弹将从静止自由下落,故导弹落地点距发射点的距离为
L=(s1+s2) cos
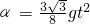
再由(s1+s2) sinα=

得t自=
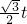 .
.答:再经过
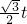 时间导弹落回地面,落地点离发射点
时间导弹落回地面,落地点离发射点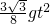 .
.分析:作出导弹匀加速直线运动的受力分析图,根据牛顿第二定律求出加速度,结合运动学公式求出t后的速度和位移,将推力的方向逆时针转动120°,根据牛顿第二定律再次求出导弹的加速度,判断出导弹的运动情况,结合运动学公式求出导弹经过时间
 的速度和位移,关闭发动机后,根据受力判断出物体的运动情况,结合运动学公式求出导弹落地的时间和落地点离发射点的位移.
的速度和位移,关闭发动机后,根据受力判断出物体的运动情况,结合运动学公式求出导弹落地的时间和落地点离发射点的位移.点评:解决本题的关键理清导弹在整个过程中的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
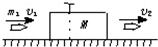 (1)下列说法中错误的是
(1)下列说法中错误的是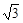 mg,使导弹沿与水平方向成
mg,使导弹沿与水平方向成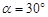 角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间
角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间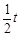 ,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).
,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).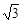 mg,使导弹沿与水平方向成
mg,使导弹沿与水平方向成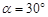 角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间
角的方向匀加速直线飞行,经过时间t后,遥控导弹的发动机保持推力的大小不变,将推力的方向逆时针转动120°,又经过时间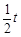 ,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).
,关闭发动机.问再经过多长时间导弹落回地面,落地点离发射点多远(不计空气的阻力和导弹本身质量的变化).