题目内容
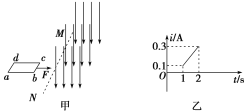
【题目】如图甲所示,宽为L、倾角为θ的平行金属导轨,下端垂直于导轨连接一阻值为R的定值电阻,导轨之间加垂直于轨道平面的磁场,其随时间变化规律如图乙所示.t=0时刻磁感应强度为B0,此时,在导轨上距电阻x1处放一质量为m、电阻为2R的金属杆,t1时刻前金属杆处于静止状态,当磁场即将减小到B1时,金属杆也即将开始下滑(金属杆所受的最大静摩擦力等于滑动摩擦力).
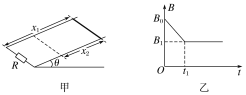
(1)求0~t1时间内通过定值电阻的电荷量;
(2)求金属杆与导轨间的最大静摩擦力;
(3)若金属杆沿导轨下滑x2后开始做匀速运动,求金属杆下滑x2过程中,电阻R产生的焦耳热.
【答案】(1) ![]()
(2)mgsinθ-![]()
(3) ![]() -
-![]()
【解析】(1)感应电动势:E=![]() =
=![]()
感应电流:I=![]()
通过定值电阻的电荷量
q=I·Δt=I·t1
即q=![]()
(2)在t1时刻,对杆有
mgsinθ-Ffm-F安=0
其中F安=B1IL
联立可得:Ffm=mgsinθ-![]()
(3)当金属杆达到最大速度时
mgsinθ-Ffm-F安′=0
即此时感应电流与0~t1时间内感应电流大小相等,感应电动势也相等.
所以B1Lv=![]()
从开始滑动到达到最大速度过程
mgx2sinθ=Q焦+Q滑+![]() mv2
mv2
其中Q滑=Ffmx2
电阻R上产生的焦耳热
QR=![]() Q焦
Q焦
解得QR=![]() -
-![]()

练习册系列答案
相关题目