��Ŀ����
5�� ��ͼ��ʾ��ˮƽ���ʹ���Ƥ���Ժ㶨���ٶ�v=2m/s�˶���һ������Ϊm=2kgС��������ֵ��м����ٶ�v=2m/s��Ƥ���˶������෴ˮƽ����Ƥ����ˮƽƤ����ΪL=4m�������Ƥ����Ķ�Ħ������Ϊ��=0.2����gȡ10m/s2����
��ͼ��ʾ��ˮƽ���ʹ���Ƥ���Ժ㶨���ٶ�v=2m/s�˶���һ������Ϊm=2kgС��������ֵ��м����ٶ�v=2m/s��Ƥ���˶������෴ˮƽ����Ƥ����ˮƽƤ����ΪL=4m�������Ƥ����Ķ�Ħ������Ϊ��=0.2����gȡ10m/s2������1�������Ƥ�����˶���ʱ��
��2�������Ƥ�����˶������������У�Ħ������������Ĺ�
��3�������Ƥ�����˶������������У���Ħ��������������
���� ��1����ţ�ٵڶ������������ļ��ٶȣ�Ȼ��Ӧ���˶�ѧ��ʽ��������˶�ʱ�䣮
��2��Ӧ�ö��ܶ������Ħ�������������Ĺ���
��3��Ӧ�������غ㶨�ɿ�������綯���˷�Ħ�������Ĺ���
��� �⣺��1�������������������Ҽ��٣����ٶȴ�СΪ a=$\frac{��mg}{m}$=��g
���ص�������ʱ��Ϊ ${t_1}=2\frac{v}{��g}=2s$
Ȼ������Ƥ�������˶����˵�ʱ��Ϊ ${t_2}=\frac{L}{2v}=1s$
�����Ƥ�����˶���ʱ�� t=t1+t2=3s
��2�������Ƥ�������������ȼ����˶������������ȼ���ֱ���˶����뿪Ƥ��ʱ���ٶȴ�С����Ƥ�����ٶ�2m/s������黬��Ƥ�����ٶȴ�С��ȣ����������Ƥ����ֹ���������˶����������Ķ��ܲ��䣬���ܵı仯Ϊ�㣬�ɶ��ܶ�����֪��Ħ�������������Ϊ0J��
��3������봫�ʹ������λ�� ${s_{���}}=\frac{{{{��2v��}^2}}}{2��g}=\frac{{2{v^2}}}{��g}$
��Ħ������������ $Q=f•{s_{���}}=��mg•\frac{{2{v^2}}}{��g}=2m{v^2}=16J$
��
��1�������Ƥ�����˶���ʱ��Ϊ2s��
��2�������Ƥ�����˶������������У�Ħ������������Ĺ�Ϊ0J��
��3�������Ƥ�����˶������������У��綯���˷�Ħ�����Ĺ�Ϊ16J��
���� ���⿼�����������˶�ʱ�䡢�����⣬������������˶���������ȷ�����ǰ����ؼ���Ӧ���ȱ����˶��˶����ɡ����ܶ����������غ㶨�ɼ�����ȷ���⣮

 �ҹ�����ġ��϶�һ�š�����������һ�������У�����˼ȶ�������2009��3��1��16ʱ13�ֳɹ�ײ�£���ͼΪ���϶�һ�š�����ײ�µ�ģ��ͼ�������ڿ��Ƶ㿪ʼ����ײ�¹켣������������������Բ���˶��Ĺ���뾶Ϊr������ΪT����������ΪG������������Ϣ������˵����ȷ���ǣ�������
�ҹ�����ġ��϶�һ�š�����������һ�������У�����˼ȶ�������2009��3��1��16ʱ13�ֳɹ�ײ�£���ͼΪ���϶�һ�š�����ײ�µ�ģ��ͼ�������ڿ��Ƶ㿪ʼ����ײ�¹켣������������������Բ���˶��Ĺ���뾶Ϊr������ΪT����������ΪG������������Ϣ������˵����ȷ���ǣ�������| A�� | ���������������� | |
| B�� | ����������϶�һ�š������� | |
| C�� | �����������ԡ��϶�һ�š����ǵ����� | |
| D�� | ���϶�һ�š������ڿ��Ƶ㴦Ӧ���� |
 �����˶�ԱͶ��ʱ����������վ��״̬�����¶�����ֱ����Ծ������߶Ⱥ����׳���ij�����˶�Ա����Ϊm��˫���뿪����ʱ���ٶ�Ϊv������˵����ȷ���ǣ�������
�����˶�ԱͶ��ʱ����������վ��״̬�����¶�����ֱ����Ծ������߶Ⱥ����׳���ij�����˶�Ա����Ϊm��˫���뿪����ʱ���ٶ�Ϊv������˵����ȷ���ǣ�������| A�� | ��վ����Ծ������У�����������Ĺ�Ϊ�� | |
| B�� | ��վ����Ծ������У�����������Ĺ�Ϊ$\frac{1}{2}$mv2 | |
| C�� | �뿪���������������У��������������� | |
| D�� | �뿪���������������У������ڳ���״̬ |
 ��ͼ��ʾ����Ͷ�������ҹ���һ�ִ�ͳͶ����Ϸ�����˺�С����ͬһ��ֱ���ϵIJ�ͬ�߶ȷֱ���ˮƽ�ٶ�v1��v2�׳�����ʸ��������Ϊ�ʵ㣩������Ͷ������ϵġ������ڣ����Կ���������������
��ͼ��ʾ����Ͷ�������ҹ���һ�ִ�ͳͶ����Ϸ�����˺�С����ͬһ��ֱ���ϵIJ�ͬ�߶ȷֱ���ˮƽ�ٶ�v1��v2�׳�����ʸ��������Ϊ�ʵ㣩������Ͷ������ϵġ������ڣ����Կ���������������| A�� | v1��v2 | B�� | v1��v2 | C�� | v1=v2 | D�� | ��ȷ�� |
| A�� | F | B�� | $\frac{F}{2}$ | C�� | $\frac{F}{4}$ | D�� | $\frac{F}{9}$ |
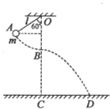 ��ͼ��ʾ������Ϊ1kg������Ϊ�ʵ�İ����ͼ�е�Aλ���ɾ�ֹ��ʼ�°ڣ����ðڵ���͵�Bλ��ʱ�߱����ϣ����߳�l=1.6m�����㵽�������ֱ�߶�ΪH=4.8m��OA��OB֮��ļн�Ϊ60�㣬g=10m/s2�����ƿ�����������
��ͼ��ʾ������Ϊ1kg������Ϊ�ʵ�İ����ͼ�е�Aλ���ɾ�ֹ��ʼ�°ڣ����ðڵ���͵�Bλ��ʱ�߱����ϣ����߳�l=1.6m�����㵽�������ֱ�߶�ΪH=4.8m��OA��OB֮��ļн�Ϊ60�㣬g=10m/s2�����ƿ����������� ��ͼ��ʾ���⻬������һ����������������������������Ϊ10cm2���������¶�Ϊ27��ʱ�����ɲ����ƵĶ���Ϊ10N���Ѿ�����ѹǿ��������ѹǿ��2��101Pa�������������Ϊ���
��ͼ��ʾ���⻬������һ����������������������������Ϊ10cm2���������¶�Ϊ27��ʱ�����ɲ����ƵĶ���Ϊ10N���Ѿ�����ѹǿ��������ѹǿ��2��101Pa�������������Ϊ���