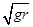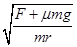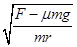题目内容
半径R=4cm的圆盘可绕圆心O水平转动，其边缘有一质量m=1kg的小物块（可视为质点），若物块随圆盘一起从静止开始加速转动，其向心加速度与时间满足a0=t2，物块与圆盘间的动摩擦因数为0.6，则：
| A．2s末圆盘的线速度大小为0.4m/s |
| B．2s末物块所受摩擦力大小为4N |
| C．物块绕完第一圈的时间约为1.88s |
| D．物块随圆盘一起运动的最大速度约为0.5m/s |
ABD
解析试题分析: 物块随圆盘做匀速圆周运动，由静摩擦力提供向心力，2S末圆盘的向心加速度a=4m/s2，根据a=ω2r，解得ω=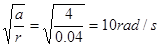
，2S末圆盘的线速度大小v=rω=0.4m/s，故A正确；由牛顿第二定律，2S末物块所受摩擦力大小Ff=ma=4N，故B正确；向心加速度与时间满足a0=t2，所以角速度与时间满足ω=
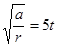。所以物块绕完第一圈平均角速度
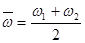=5rad/s，所以物块绕完第一圈的时间t=
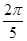=1.25s，故C正确；物块随圆盘一起运动的最大速度时，静摩擦力是最大静摩擦力，μmg=
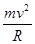，解得：v=
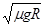=0.49m/s，约为0.5m/s，所以D正确；
考点： 匀速圆周运动；向心加速度
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案质量为m的小球,用长为l的细线悬挂在O点,在O点的正下方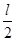
处有一光滑的钉子P,把小球拉到与钉子P等高的位置,摆线被钉子挡住.如图所示,让小球从静止释放,当小球第一次经过最低点时（ ） 
| A．小球运动的线速度突然减小 | B．小球的角速度突然减小 |
| C．小球的向心加速度突然减小 | D．悬线的拉力突然增大 |
如图所示，一个匀速转动的半径为r的水平圆盘上放着两个小木块M和N，木块M放在圆盘的边缘处，木块N放在离圆心
处，它们都随圆盘一起运动。下列说法中正确的是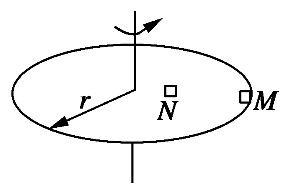
| A．M受到重力、支持力、向心力 |
| B．M、N两木块的线速度相等 |
| C．M的角速度是N的3倍 |
| D．M的向心加速度是N的3倍 |
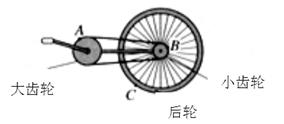
“嫦娥三号”探月卫星于2013年12月2日1点30分在西昌卫星发射中心发射，将实现“落月”的新阶段。若已知引力常量G，月球绕地球做圆周运动的半径r1、周期T1“嫦娥三号”探月卫星绕月球做圆周运动的环月轨道(见图)半径r2、周期T2，不计其他天体的影响，则根据题目条件可以( )
| A．求出“嫦娥三号”探月卫星的质量 |
| B．求出地球与月球之间的万有引力 |
| C．求出地球的密度 |
D．得出 |
如图所示，水平放置的两个用相同材料制成的轮P和Q靠静摩擦传动，两轮的半径R∶r＝2∶1，当主动轮Q匀速转动的角速度为ω1时，在Q轮边缘上放置的小木块恰能相对静止，若把小木块放在P轮边缘上，改变Q轮转动的角速度至ω2时，小木块也恰能静止，则( )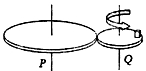
A．ω1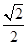＝ ω2 | B．ω1＝ω2 |
C．ω1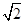＝ ω2 | D．ω1＝2ω2 |
