Question

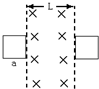如图所示，在光滑的水平面上，有竖直向下的匀强磁场，分布在宽度为L的区域里．现有一边长为a（a＜L的正方形闭合线圈刚好能穿过磁场，则线圈在滑进磁场过程中产生的热量Q₁与滑出磁场过程中产生的热量Q₂之比为（　　）

A．1：1

B．2：1

C．3：1

D．4：1

Answer 1

分析：运用微分的思想求出线圈进磁场和出磁场过程中速度变化量的大小，再根据能量守恒求出线圈在滑进磁场过程中产生的热量Q₁与滑出磁场过程中产生的热量Q₂之比．

解答：解：线圈在进磁场或出磁场某一位置的加速度a=

BIa

m

=

B2a2v

mR

，则在很短时间内速度的变化量△v=a△t=

B2a2

mR

v△t=

B2a2

mR

△x，△v=

B2a2

mR

△x，解得△v=

B2a3

mR

，知进磁场和出磁场速度的变化量大小相等．设进磁场的速度为v，则完全进磁场的速度为

v

2

，完全出磁场的速度为0．根据能量守恒定律得，Q1=

1

2

mv2-

1

2

m(

v

2

)2=

3

8

mv2，Q2=

1

2

m(

v

2

)2=

1

8

mv2，所以

Q1

Q2

=

3

1

．故C正确，A、B、D错误．
故选C．

点评：解决本题的难点在于通过微分的思想得出线圈进磁场和出磁场过程中速度变化量大小相等．然后通过能量守恒进行求解．