题目内容
弹性小球从离地高度为H处自由下落到水平地面,碰撞后弹起,由于小球在与地面的碰撞过程中总有机械能损失,且损失量与碰撞时的速度有关,故每次碰撞后上升高度总是前一次的0.64倍.不计空气阻力,重力加速度为g,求:(1)小球落地时的速度大小v1与碰撞后弹起的速度大小v2之比;
(2)若要使小球从原处下落后仍能上升到原来高度,则小球在开始下落时需要的最小初速度v.
【答案】分析:小球下落过程中,重力做正功,空气阻力做负功,根据动能定理分别对两种进行研究列式,即可求出小球应需多大的初速度.
解答:解:(1)对下落和上升的两个过程运用动能定理得:
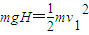
0.64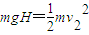
解得: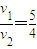
(2)设空气阻力大小为f,则:
mg?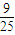 H-f
H-f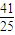 H=0
H=0
-f?2H=0-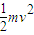
解得:v=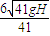
答:(1)小球落地时的速度大小v1与碰撞后弹起的速度大小v2之比为5:4;
(2)若要使小球从原处下落后仍能上升到原来高度,则小球在开始下落时需要的最小初速度为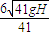 .
.
点评:本题涉及力在空间的效果,首先考虑运用动能定理,也可以由牛顿第二定律和运动学公式结合求解.
解答:解:(1)对下落和上升的两个过程运用动能定理得:
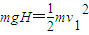
0.64
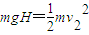
解得:
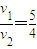
(2)设空气阻力大小为f,则:
mg?
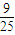 H-f
H-f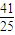 H=0
H=0-f?2H=0-
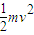
解得:v=
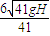
答:(1)小球落地时的速度大小v1与碰撞后弹起的速度大小v2之比为5:4;
(2)若要使小球从原处下落后仍能上升到原来高度,则小球在开始下落时需要的最小初速度为
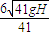 .
.点评:本题涉及力在空间的效果,首先考虑运用动能定理,也可以由牛顿第二定律和运动学公式结合求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目