题目内容
 (2010?上海模拟)两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点,B点为轨道最低点,O为圆心,轨道各处光滑且固定在竖直平面内.质量均为m的两小环P、Q用长为
(2010?上海模拟)两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点,B点为轨道最低点,O为圆心,轨道各处光滑且固定在竖直平面内.质量均为m的两小环P、Q用长为| 2 |
(1)当P环运动到B点时,系统减少的重力势能△EP;
(2)当P环运动到B点时的速度v;
(3)在运动过程中,P环能达到的最大速度vm;
(4)若将杆换成长2
| 2 |
分析:(1)轻杆下滑过程,系统的机械能守恒,确定出两环下降的高度,即可由求得△EP;
(2)P、Q都进入圆轨道后,两环具有相同角速度,两环速度大小一定相等,根据系统的机械能守恒列式求解最大速度.
(3)当系统质心下降到最低处时,系统达到的速度最大,此时MN离O点竖直高度为
R,再由机械能守恒求解.
(4)由于杆长超过了半圆直径,故A环一直在下方,速度为零时,结合几何关系并根据机械能守恒定律列方程求解即可求解出高度.
(2)P、Q都进入圆轨道后,两环具有相同角速度,两环速度大小一定相等,根据系统的机械能守恒列式求解最大速度.
(3)当系统质心下降到最低处时,系统达到的速度最大,此时MN离O点竖直高度为
| ||
| 2 |
(4)由于杆长超过了半圆直径,故A环一直在下方,速度为零时,结合几何关系并根据机械能守恒定律列方程求解即可求解出高度.
解答:解:(1)当P环运动到B点时,系统减少的重力势能 △Ep=WGM+WGN=mg2R+mg(1+
)R=(3+
)mgR
(2)P、Q都进入圆轨道后,两环具有相同角速度,则两环速度大小一定相等
整体的机械能守恒,则有:△EP=△EK
则得 (3+
)mgR=
2mv2
得到 v=
(3)当系统质心下降到最低处时,系统达到的速度最大,此时MN离O点竖直高度为
R
则有(1+
)mgR+(
+1+
)mgR=
?2m
得到 v=
(4)由于杆超过了半圆直径,所以两环运动如图.
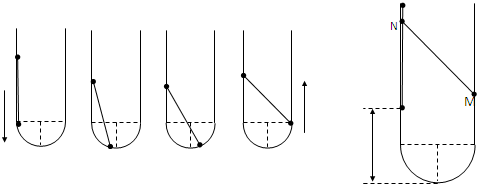
M再次上升后,设位置比原来高h,如图所示.
由机械能守恒:-mgh+mg(2
R-2R-h)=0
解得h=(
-1)R,
P环能达到的最大高度H=(
+1)R
答:
(1)当P环运动到B点时,系统减少的重力势能△EP是(3+
)mgR.
(2)当P环运动到B点时的速度v是
.
(3)在运动过程中,P环能达到的最大速度vm是
.
(4)若将杆换成长2
R,P环仍从原处由静止释放,经过半圆型底部再次上升后,P环能达到的最大高度H是(
+1)R.
| 2 |
| 2 |
(2)P、Q都进入圆轨道后,两环具有相同角速度,则两环速度大小一定相等
整体的机械能守恒,则有:△EP=△EK
则得 (3+
| 2 |
| 1 |
| 2 |
得到 v=
(3+
|
(3)当系统质心下降到最低处时,系统达到的速度最大,此时MN离O点竖直高度为
| ||
| 2 |
则有(1+
| ||
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| v | 2 m |
得到 v=
(2+2
|
(4)由于杆超过了半圆直径,所以两环运动如图.

M再次上升后,设位置比原来高h,如图所示.
由机械能守恒:-mgh+mg(2
| 2 |
解得h=(
| 2 |
P环能达到的最大高度H=(
| 2 |
答:
(1)当P环运动到B点时,系统减少的重力势能△EP是(3+
| 2 |
(2)当P环运动到B点时的速度v是
(3+
|
(3)在运动过程中,P环能达到的最大速度vm是
(2+2
|
(4)若将杆换成长2
| 2 |
| 2 |
点评:本题关键是根据几何关系多次得到环的具体位置,然后根据机械能守恒定律列方程求解即可.

练习册系列答案
相关题目
 (2010?上海模拟)如图所示,水平方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5 C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线
(2010?上海模拟)如图所示,水平方向的平行线表示匀强电场的电场线,但未标明方向.电场中有一个带正电荷的微粒,电量为10-5 C,若该带电微粒仅受电场力的作用,从M点运动到N点时,动能减少了10-3 J,则该电荷运动轨迹应为虚线