题目内容
10.设地球绕太阳做匀速圆周运动,半径为R,速度为v.而太阳围绕银河系中心的运动也可视为匀速圆周运动,其运动速度约为地球公转速度的7倍,轨道半径约为地球公转轨道半径的2×109倍.为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量.(万有引力常量用G表示)(1)求:太阳的质量.
(2)估算银河系中恒星的个数.
分析 研究地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量.
研究太阳绕银河系运动,由万有引力充当向心力得出银河系质量.
解答 解:研究地球绕太阳做圆周运动的向心力,由太阳对地球的万有引力充当.根据万有引力定律和牛顿第二定律有:
$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$,
整理得:$M=\frac{{v}^{2}R}{G}$
太阳绕银河系运动也是由万有引力充当向心力,同理可得:
$M′=\frac{(7v)^{2}R′}{G}=\frac{49{v}^{2}×2×1{0}^{9}R}{G}$=$9.8×1{0}^{10}\frac{{v}^{2}R}{G}$=9.8×1010M
所以,银河系中恒星数目约为:
N=$\frac{M′}{M}=9.8×1{0}^{10}≈1{0}^{11}$个
答:(1)太阳的质量为$\frac{{v}^{2}R}{G}$;
(2)银河系中恒星数目约为1011个.
点评 该题考查万有引力定律的一般应用,明确研究对象,根据万有引力提供向心力找出中心体的质量.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
20.用手握住一个酱油瓶,酱油瓶开口向上静止在手中不动.以下各种说法正确的是( )
| A. | 酱油瓶静止在手中,受到了静摩擦力的作用 | |
| B. | 随着手握酱油瓶的力增大,瓶子所受到的静摩擦力将增大 | |
| C. | 手握酱油瓶的力增大时,瓶子所受到的静摩擦力并未增大 | |
| D. | 向酱油瓶内逐渐注水,若瓶子仍静止,瓶所受的静摩擦力将增大 |
18.地球绕太阳的运动轨道可近似成圆形,已知质量m的地球绕太阳作半径是r的匀速圆周远动,估测太阳的质量时还要用到( )
| A. | 地球的自转周期T(1天) | B. | 月球的公转周期T(农历1个月) | ||
| C. | 地球的公转周期T(1年) | D. | 地球表面的重力加速度(10m/s2) |
15.关于电磁感应现象,下列说法中正确的是( )
| A. | 只要有磁通量穿过电路,电路中就有感应电流 | |
| B. | 只要闭合电路在磁场中运动,电路中就有感应电流 | |
| C. | 只要穿过闭合电路的磁通量足够大,电路中就一定能产生感应电流 | |
| D. | 只要穿过闭合电路的磁通量发生变化,电路中就一定有感应电流 |
2. 如图所示,以10m/s的初速度水平抛出的物体,飞行一段时间后,垂直撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是(g=10m/s2)( )
如图所示,以10m/s的初速度水平抛出的物体,飞行一段时间后,垂直撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是(g=10m/s2)( )
 如图所示,以10m/s的初速度水平抛出的物体,飞行一段时间后,垂直撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是(g=10m/s2)( )
如图所示,以10m/s的初速度水平抛出的物体,飞行一段时间后,垂直撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是(g=10m/s2)( )| A. | $\frac{\sqrt{3}}{3}$S | B. | $\frac{2\sqrt{3}}{3}$S | C. | $\sqrt{3}$S | D. | 2S |
19. 质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )
质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )
 质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )
质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )| A. | 外力对物体做的总功为零 | B. | 重力对物体做功为mg(H+h) | ||
| C. | 重力对物体做功为mgH | D. | 地面对物体平均阻力为$\frac{mg(H+h)}{h}$ |
20.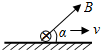 如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )
如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )
 如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )
如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )| A. | 当α=90°时安培力最小 | |
| B. | 当α=150°时磁感应强度最小 | |
| C. | 若磁感应强度大小为定值,在α<90°的前提下增大α,则金属棒将做匀减速运动 | |
| D. | 若磁感应强度大小为定值,在α<90°的前提下增大α,则金属棒将做加速运动 |
