题目内容
1.如图甲所示,A和B是长为L、间距为d的平行金属板,靶MN垂直固定在它们的右端.在A、B板上加上方形波电压,如图乙所示.电压的正向值为U0,反向值为$\frac{{U}_{0}}{2}$,周期为T.现有质量为m、带电量为+q的粒子连续从AB的中点O以平行于金属板的方向射入.设所有粒子都能穿过电场打到靶上,而且每个粒子在AB间的飞行时间均为T,不计粒子重力的影响.试问: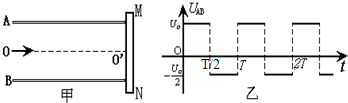
(1)粒子射入平行金属板时的速度多大?
(2)t=$\frac{T}{2}$时刻入射的粒子打到靶上的位置距靶中心点O′多远?
分析 (1)粒子在电场中受到竖直向下的电场力,水平方向不受力而做匀速直线运动,由T=$\frac{L}{v}$ 可求速度;
(2)入射的粒子打到靶上的位置距靶中心点O′多远与粒子竖直方向的分位移有关.分析粒子在竖直方向的运动:$\frac{T}{2}$~T时间内,粒子向上作初速为零的匀加速运动,在T~$\frac{3}{2}$T时间内,由于此时的加速度大小a′=2a,所以粒子先向上减速后向下加速,根据牛顿第二定律和运动学公式结合求竖直方向的总位移,即可确定粒子打到靶上的位置.
解答 解:(1)粒子在水平方向粒子作匀速直线运动,则有:v0=$\frac{L}{T}$
(2)在竖直方向,从$\frac{T}{2}$~T时间内,粒子向上作初速为零的匀加速运动,有:
a=$\frac{q•\frac{{U}_{0}}{2}}{md}$=$\frac{q{U}_{0}}{md}$
则粒子竖直方向上的位移:
s1=$\frac{1}{2}$a($\frac{T}{2}$ )2=$\frac{q{U}_{0}{T}^{2}}{16md}$
粒子在T~$\frac{3}{2}$T时间内,由于此时的加速度大小a′=2a,所以粒子先向上减速后向下加速,此阶段竖直方向的位移s2=0.
综上所述,有竖直方向上总位移 s总=s1+s2=$\frac{q{U}_{0}{T}^{2}}{16md}$
答:(1)粒子射入平行金属板时的速度为$\frac{L}{T}$;
(2)t=$\frac{T}{2}$时刻入射的粒子打到靶上的位置距靶中心点O′距离为$\frac{q{U}_{0}{T}^{2}}{16md}$.
点评 本题是粒子在周期性变化的电场中运动,分析带电粒子的运动情况是关键,并能运用牛顿第二定律和运动学结合进行求解.

 阅读快车系列答案
阅读快车系列答案| A. | 空气泡对光线有发散作用 | |
| B. | 空气泡对光线有会聚作用 | |
| C. | 从水中或玻璃中射到空气泡界面处的光一部分发生全反射形成的 | |
| D. | 从空气泡到达水或玻璃与气泡分界面处的光一部分发生全反射形成的 |
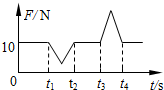 某中学物理实验小组利用数字化信息实验室系统,观察超重和失重现象.他们在学校电梯内做实验,在电梯顶板上固定一个测量力大小的传感器,测量挂钩向下,并在钩上悬挂一个重为10N的钩码.在电梯运动过程中,计算机显示屏上显示出如图所示F-t图线.根据图线分析可知下列说法中正确的是 ( )
某中学物理实验小组利用数字化信息实验室系统,观察超重和失重现象.他们在学校电梯内做实验,在电梯顶板上固定一个测量力大小的传感器,测量挂钩向下,并在钩上悬挂一个重为10N的钩码.在电梯运动过程中,计算机显示屏上显示出如图所示F-t图线.根据图线分析可知下列说法中正确的是 ( )| A. | 从时刻t1到t2,钩码处于超重状态,从时刻t3到t4,钩码处于失重状态 | |
| B. | t1到t2时间内,电梯一定正在向下运动,t3到t4时间内,电梯可能正在向上运动 | |
| C. | t1到t4时间内,电梯可能先加速向下运动,接着匀速向下运动,再减速向下运动 | |
| D. | t1到t4时间内,电梯可能先加速向上运动,接着匀速向上运动,再减速向上运动 |

 如图所示,已知电源电动势E=18V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L和内阻r′=0.5Ω的小型直流电动机恰能正常工作,求
如图所示,已知电源电动势E=18V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L和内阻r′=0.5Ω的小型直流电动机恰能正常工作,求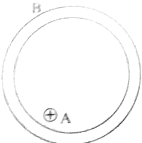 如图所示,A为带正电的金属球,B为不带电的金属球壳,试分别讨论下列几种情况下,A球和B球内外表面的带电情况:
如图所示,A为带正电的金属球,B为不带电的金属球壳,试分别讨论下列几种情况下,A球和B球内外表面的带电情况: