题目内容
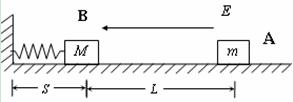
如图所示,在绝缘水平面上放一质量m = 2.0×10-3kg的带电滑块A,所带电荷量q = 1.0×10-7C.在滑块A的左边L = 0.3m处放置一个不带电的绝缘滑块B,质量M = 4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,此后两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
(1)两滑块碰撞后刚结合在一起的共同速度v;
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s.w_w*w.k*s_5 u.c*o m
(1) v=1.0m/s (2分)
(2) ![]() … (3分)
… (3分)
解析:
(1)设两滑块碰前A的速度为v1,由动能定理有:
![]() (2分) 解得: v1=3m/s (2分)
(2分) 解得: v1=3m/s (2分)
B两滑块碰撞,由于时间极短动量守恒,设共同速度为v
![]() (2分) 解得: v=1.0m/s (2分)
(2分) 解得: v=1.0m/s (2分)
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理有:
![]() .(2分) 解得: w_w*w.k*s_5 u.c*o m x1=0.02m (2分)
.(2分) 解得: w_w*w.k*s_5 u.c*o m x1=0.02m (2分)
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:
![]() (2分) 解得: x2≈0.05m (2分)
(2分) 解得: x2≈0.05m (2分)
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离为:
![]() … (3分)
… (3分)

练习册系列答案
相关题目
 如图所示,在绝缘水平面上,相距为L的A、B两点处分别固定着两个等量正电荷.a、b是AB连线上两点,其中Aa=Bb=
如图所示,在绝缘水平面上,相距为L的A、B两点处分别固定着两个等量正电荷.a、b是AB连线上两点,其中Aa=Bb= (2009?德阳模拟)如图所示,在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边L=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,此后两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
(2009?德阳模拟)如图所示,在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边L=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,此后两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求: (2008?天津模拟)如图所示,在绝缘水平面上固定两个等量同种电荷A、B,在AB连线上的P点释放一带电滑块,则滑块会由静止开始一直向右运动到AB连线上的另一点M而静止.则以下判断正确的是( )
(2008?天津模拟)如图所示,在绝缘水平面上固定两个等量同种电荷A、B,在AB连线上的P点释放一带电滑块,则滑块会由静止开始一直向右运动到AB连线上的另一点M而静止.则以下判断正确的是( ) (2012?黄埔区模拟)如图所示,在绝缘水平面上A、B两点分别固定一个电荷量相等的同种点电荷,在AB连线上靠近A点的P点由静止释放一个带电小滑块,滑块会由静止开始一直向右运动到AB连线上的某一点M(图中没有画出)而静止不动.下列说法中正确的是( )
(2012?黄埔区模拟)如图所示,在绝缘水平面上A、B两点分别固定一个电荷量相等的同种点电荷,在AB连线上靠近A点的P点由静止释放一个带电小滑块,滑块会由静止开始一直向右运动到AB连线上的某一点M(图中没有画出)而静止不动.下列说法中正确的是( ) (2008?广州一模)如图所示,在绝缘水平面上,相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点,C、D是AB连线上两点,其中AC=CO=OD=DB=
(2008?广州一模)如图所示,在绝缘水平面上,相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点,C、D是AB连线上两点,其中AC=CO=OD=DB=