题目内容
 (2008?广州一模)如图所示,在绝缘水平面上,相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点,C、D是AB连线上两点,其中AC=CO=OD=DB=
(2008?广州一模)如图所示,在绝缘水平面上,相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点,C、D是AB连线上两点,其中AC=CO=OD=DB=| 1 | 4 |
(1)小滑块与水平面之间的动摩擦因数μ;
(2)C、O两点间的电势差UCO;
(3)小滑块运动的总路程S.
分析:(1)C、D两点电势相等,故滑块从C到D的过程中,电场力不做功,只有摩擦力做功,则由动能定理可求得动摩擦因数μ;
(2)滑块在b点时,受A、B的库仑力及摩擦力,由牛顿第二定律可求得加速度;
(3)由题意可知物体应停在O点,由动能定理可求得从a到o点时电场力所做的功,则对全程由动能定理可求得滑块滑动的总路程.
(2)滑块在b点时,受A、B的库仑力及摩擦力,由牛顿第二定律可求得加速度;
(3)由题意可知物体应停在O点,由动能定理可求得从a到o点时电场力所做的功,则对全程由动能定理可求得滑块滑动的总路程.
解答:解:(1)由于C点与D点等势,滑块从C到D的过程中,电场力不做功,则小滑块第一次由C到D,由动能定理有:
-μmg?
=0-E0
求得,小滑块与水平面间动摩擦因数为 μ=
;
(2)由C第一次到O时,由动能定理得
-μmg?
+qUCO=nE0-E0,
解得,UCO=
(3)由C开始到最后停在O点,有:qUCO-μmgS=0-E0
由以上二式得:S=
故小滑块运动的总距离为:S=
答:
(1)小滑块与水平面之间的动摩擦因数μ为
;
(2)C、O两点间的电势差UCO为
.
(3)小滑块运动的总路程S为
.
-μmg?
| L |
| 2 |
求得,小滑块与水平面间动摩擦因数为 μ=
| 2E0 |
| mgL |
(2)由C第一次到O时,由动能定理得
-μmg?
| L |
| 4 |
解得,UCO=
| (2n-1)E0 |
| 2q |
(3)由C开始到最后停在O点,有:qUCO-μmgS=0-E0
由以上二式得:S=
| (2n+1)L |
| 4 |
故小滑块运动的总距离为:S=
| (2n+1)L |
| 4 |
答:
(1)小滑块与水平面之间的动摩擦因数μ为
| 2E0 |
| mgL |
(2)C、O两点间的电势差UCO为
| (2n-1)E0 |
| 2q |
(3)小滑块运动的总路程S为
| (2n+1)L |
| 4 |
点评:电场中的动能定理的应用要注意电场力做功和路径无关,只和初末两点的电势差有关,故很容易可求得电场力的功.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目


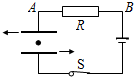 (2008?广州一模)如图所示,平行板电容器在充电后不切断电源,此时板间有一带电油滴恰能在电场中静止,当正对的平行板左右错开一些时( )
(2008?广州一模)如图所示,平行板电容器在充电后不切断电源,此时板间有一带电油滴恰能在电场中静止,当正对的平行板左右错开一些时( ) (2008?广州一模)如图(a)所示,竖直轻弹簧下端与放在水平地面上的物块A相连.上端与物块B相连.物块C在B的正上方某处自由落下,与B碰撞后粘合在一起.在物块C正上方放置一个速度传感器,以测量C下落的速度vC;在物块A的正下方放置一个压力传感器,以测量物块A对地面的压力N,得到如图(b)所示v-t和N-t图线,图中纵坐标轴上的P、v1、v2为已知量.已知弹簧的劲度系数为k,A、B、C三个物块的质量相等且都可视为质点,重力加速度为g,求:
(2008?广州一模)如图(a)所示,竖直轻弹簧下端与放在水平地面上的物块A相连.上端与物块B相连.物块C在B的正上方某处自由落下,与B碰撞后粘合在一起.在物块C正上方放置一个速度传感器,以测量C下落的速度vC;在物块A的正下方放置一个压力传感器,以测量物块A对地面的压力N,得到如图(b)所示v-t和N-t图线,图中纵坐标轴上的P、v1、v2为已知量.已知弹簧的劲度系数为k,A、B、C三个物块的质量相等且都可视为质点,重力加速度为g,求: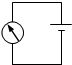 (2008?广州一模)(多选题)为了研究磁通量变化时感应电流的方向,先通过如图所示确定电流通过检流计时指针的偏转方向.下面为实验过程的示意图,竖直放置的线圈固定不动,将条形磁铁从线圈上方插入或拔出,线圈和检流计构成的闭合回路中就会产生感应电流.各图中分别标出了磁铁的极性、磁铁相对线圈的运动方向以及线圈中产生的感应电流的方向等情况,其中方向关系正确的是 ( )
(2008?广州一模)(多选题)为了研究磁通量变化时感应电流的方向,先通过如图所示确定电流通过检流计时指针的偏转方向.下面为实验过程的示意图,竖直放置的线圈固定不动,将条形磁铁从线圈上方插入或拔出,线圈和检流计构成的闭合回路中就会产生感应电流.各图中分别标出了磁铁的极性、磁铁相对线圈的运动方向以及线圈中产生的感应电流的方向等情况,其中方向关系正确的是 ( )