题目内容
如图所示，A是地球的同步卫星，另一卫星B的圆轨道位于赤道平面内，离地面高度为h。已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心。
(1)求卫星B的运行周期；
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们再一次相距最近？
（1）2π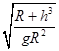
（2）
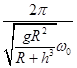
解析:(1)由万有引力定律和向心力公式得
G
＝m
(R＋h)(2分)
在地球表面处有G
＝mg(2分) 联立得TB＝2π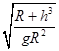①(2分)
(2)B转动的角速度大于A，因此当A、B再次相距最近时，B比A多转一周，即多转2π弧度，故(ωB－ωA)t＝2π(2分)
又ωB＝
＝
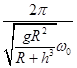(1分) 把①代入得t＝.(1分)
练习册系列答案
名校课堂系列答案
相关题目
（2006?江苏）如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h．已知地球半径为R，地球自转角速度为ωo，地球表面的重力加速度为g，O为地球中心．
如图所示，A是地球的同步卫星，已知地球半径为R，地球自转角速度为ω，地球表面的重力加速度为g．
如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h．已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．
（2013?河南模拟）如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h．已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．关于AB两卫星的下列叙述正确的是（ ）
