题目内容
 如图所示,A是地球的同步卫星,已知地球半径为R,地球自转角速度为ω,地球表面的重力加速度为g.
如图所示,A是地球的同步卫星,已知地球半径为R,地球自转角速度为ω,地球表面的重力加速度为g.(1)求出同步卫星离地面高度h
(2)求出地球的密度ρ(已知引力常量为G)
分析:(1)同步卫星和地球同步,其周期为地球自转的周期,根据万有引力提供向心力及万有引力和向心力的公式中的角速度公式即可求解;
(2)对于在地面处的物体有万有引力等于物体重力,表示出地球的质量,再根据密度公式求解.
(2)对于在地面处的物体有万有引力等于物体重力,表示出地球的质量,再根据密度公式求解.
解答:解:(1)设地球的质量为M,对于在地面处质量为m的物体有:G
=m g①
设同步卫星的质量为m,则:G
=mω2(R+h)②
由①②两式解得:h=
-R
(2)又因为:ρ=
③
由①③两式解得:ρ=
答:(1)同步卫星离地面高度是
-R
(2)地球的密度是
.
| Mm |
| R2 |
设同步卫星的质量为m,则:G
| Mm |
| (R+h)2 |
由①②两式解得:h=
| 3 |
| ||
(2)又因为:ρ=
| M | ||
|
由①③两式解得:ρ=
| 3g |
| 4πGR |
答:(1)同步卫星离地面高度是
| 3 |
| ||
(2)地球的密度是
| 3g |
| 4πGR |
点评:该题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中注意黄金代换式G
=m0g的应用.
| Mm0 |
| R2 |

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
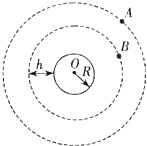 (2006?江苏)如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ωo,地球表面的重力加速度为g,O为地球中心.
(2006?江苏)如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ωo,地球表面的重力加速度为g,O为地球中心.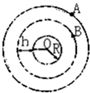 如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.
如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.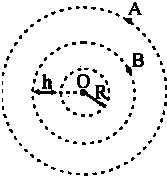 (2013?河南模拟)如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.关于AB两卫星的下列叙述正确的是( )
(2013?河南模拟)如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.关于AB两卫星的下列叙述正确的是( )