题目内容
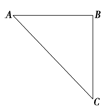
【题目】如图所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，B点为水平面与轨道的切点，在离B距离为x的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点：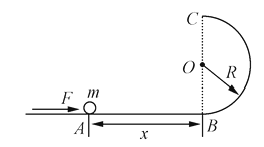
（1）求推力对小球所做的功。
（2）x取何值时，完成上述运动推力所做的功最少？最小功为多少。
（3）x取何值时，完成上述运动推力最小？最小推力为多少。
【答案】
（1）
质点从半圆弧轨道做平抛运动又回到A点，设质点在C点的速度为vC，质点从C点运动到A点所用的时间为t，
在水平方向： x=vCt 竖直方向上：2R= 
gt2 解得 
对质点从A到C由动能定理有 WF-mg·2R= 
解得： 
（2）
要使F力做功最少，确定x的取值，由WF=2mgR+ mv 
知，只要质点在C点速度最小，则功WF就最小。若质点恰好能通过C点，其在C点最小速度为v，由牛顿第二定律有 
,则v= 
有 
，解得：x=2R
当x=2R时， WF最小，最小的功：WF= 
mgR
（3）
由式 ) 及WF=Fx得： 
)
F有最小值的条件是： 
即x=4R
得最小推力为：F=mg.
【解析】（1）质点从半圆弧轨道做平抛运动又回到A点，设质点在C点的速度为vC ， 质点从C点运动到A点所用的时间为t ，
在水平方向： x=vCt 竖直方向上：2R= gt2 解得
对质点从A到C由动能定理有 WF-mg·2R=
解得： （2）要使F力做功最少，确定x的取值，由WF=2mgR+ mv 知，只要质点在C点速度最小，则功WF就最小。若质点恰好能通过C点，其在C点最小速度为v ， 由牛顿第二定律有 ,则v=
有 ，解得：x=2R
当x=2R时， WF最小，最小的功：WF= mgR（3）由式 ) 及WF=Fx得： )
F有最小值的条件是： 即x=4R
得最小推力为：F=mg.
本题考查了牛顿第二定律的应用
