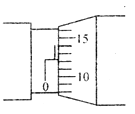
��Ŀ����
����Ŀ����ͼ��ʾ���㹻���Ĺ⻬ƽ�н�������MN��PQ��ֱ���ã�һ���Ÿ�Ӧǿ��B=0.50T����ǿ�ų���ֱ��������ƽ�棬������϶�M��P��������ֵΪR=0.30���ĵ��裬�������L=0.40m������Ϊr=0.20���Ľ�����ab�����ڵ����ϣ�������費�ƣ���ʹ������ab�ɾ�ֹ��ʼ�»�0.7m ����5m/s���ٶ������˶�����g=10m/s2��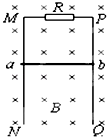
��
��1��������������m��
��2���ڵ��������2.70m�ڣ���·�в���������Q��
���𰸡�
��1���⣺�ӱ��������ݿ�֪����ֹ��ʼ�»�0.7m ����5m/s���ٶ������˶����綯��ΪE����·�еĵ���ΪI���������ܵ��İ�����ΪF����
E=BLv
I= ![]()
F=BIL=mg
���Ͻ�ã�m= ![]() =
= ![]() ��
��
�𣺽�����������mΪ0.04kg��
��2���⣺�����»������У��������Ͱ������������˷����������Ĺ����ڻ�·�Ľ����ȣ����������غ�ã�
mgh2= ![]() mv2+Q
mv2+Q
�������ݽ��Q=0.58J��
�𣺵���R�ϲ���������Ϊ0.58J��
����������1���������֪����0.7m����������˶��������½��ĸ߶Ⱥ�ʱ���������ֱ���˶����ٶȣ�ץס�����Ͱ�����ƽ�⣬����и�����ĸ�Ӧ�綯�ƺͱպϵ�·ŷķ�����������������������2���������2.7m�ڽ������������ܵļ�С��ת��Ϊ�������Ķ��ܺ�������·��������R�����������������������غ㶨���������R�ϲ�����������
�����㾫����������Ĺؼ����������Ÿ�Ӧ��������֪ʶ�����յ�Ÿ�Ӧ�����ʵ���Dz�����Ӧ�綯�ƣ������·�պϣ����и�Ӧ��������·���պϣ���ֻ�и�Ӧ�綯�ƶ���Ӧ�������Լ��Ե�Ÿ�Ӧ���·�����⣬�˽��÷����ڵ�Ÿ�Ӧ���ɺ���ζ���ȷ����Ӧ�綯�ƵĴ�С�ͷ�����Ч��·������ȫ��·ŷķ���ɣ���������·���ʣ��繦�ʵȹ�ʽ������⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�