题目内容
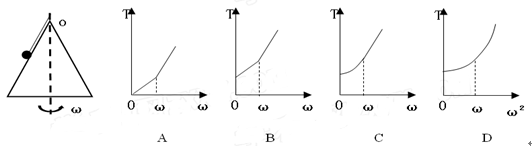
如图所示，甲、乙两水平圆盘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲转动，接触处无相对滑动。甲圆盘与乙圆盘的半径之比为r甲∶r乙＝3∶1，两圆盘和小物体m1、m2之间的动摩擦因数相同，m1距O点为2r，m2距O′点为r，当甲缓慢转动起来且转速慢慢增加时（ ） 
| A．滑动前m1与m2的角速度之比ω1∶ω2＝1∶3 |
| B．滑动前m1与m2的向心加速度之比a1∶a2＝1∶3 |
| C．随转速慢慢增加，m1先开始滑动 |
| D．随转速慢慢增加，m2先开始滑动 |
AD
解析试题分析：甲、乙两轮子边缘上的各点线速度大小相等，有：ω1?3r=ω2?r，则得ω甲：ω乙=1：3，所以物块相对盘开始滑动前，m1与m2的角速度之比为1：3．故A正确；物块相对盘开始滑动前，根据a=ω2r得：m1与m2的向心加速度之比为 a1：a2=ω12?2r：ω22r=2：9，故B错误．根据μmg=mrω2知，临界角速度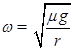
，可知甲乙的临界角速度之比为1：
，甲乙线速度相等，甲乙的角速度之比为ω甲：ω乙=1：3，可知当转速增加时，乙先达到临界角速度，所以乙先开始滑动．故D正确，C错误．故选：AD．
考点：圆周运动；牛顿定律；向心加速度。
关于牛顿运动定律，以下说法中正确的是（ ）
| A．运动越快的汽车越不容易停下来，是因为汽车运动得越快，惯性就越大 |
| B．人从水平地面上猛得竖直向上跳起，地面对人的支持力将会大于人对地面的压力 |
| C．N/kg与m/s2都是加速度的国际制单位 |
| D．物体的加速度方向有时与合外力方向相同，有时与合外力方向相反 |
一个在光滑水平面上运动的物体，如果在运动方向上受到一个逐渐减小的力的作用，力的方向与速度的方向相同，则物体的加速度大小和速度大小的变化情况是（ ）
| A．加速度逐渐减小，速度逐渐增大 | B．加速度逐渐减小，速度逐渐减小 |
| C．加速度逐渐增大，速度逐渐增大 | D．加速度逐渐增大，速度逐渐减小 |
如图所示，长为l的细绳一端固定在O点，另一端拴住一个小球，在O点的正下方与O点相距的地方有一枚与竖直平面垂直的钉子；把小球拉起使细绳在水平方向伸直，由静止开始释放，当细绳碰到钉子的瞬间，下列说法正确的是 （ ）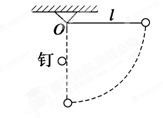
| A．小球的线速度不发生突变 |
| B．小球的角速度突然增大到原来的2倍 |
| C．小球的向心加速度突然增大到原来的2倍 |
| D．绳子对小球的拉力突然增大到原来的2倍 |
如图所示，一根轻弹簧下端固定，竖立在水平面上。其正上方A位置有一只小球。小球从静止开始下落，在B位置接触弹簧的上端，在C位置小球所受弹力大小等于重力，在D位置小球速度减小到零。小球下降阶段下列说法中正确的是：
| A．在B位置小球速度最大 |
| B．在C位置小球速度最大 |
| C．从A→C位置小球重力势能的减少量小于重力做的功 |
| D．从A→D位置小球重力势能的减少等于弹簧弹性势能的增加 |
质量为m、电荷量为q的带正电小球，从倾角为θ的粗糙绝缘斜面（µ<tanθ）上由静止下滑，斜面足够长，整个斜面置于方向水平向外的匀强磁场中，其磁感强度为B，如图所示。带电小球运动过程中，下面说法中正确的是
| A．小球在斜面上运动时做匀加速直线动 |
| B．小球在斜面上运动时做加速度增大，而速度也增大的变加速直线运动 |
| C．小球最终在斜面上匀速运动 |
D．小球在斜面上下滑过程中，当小球对斜面压力刚好为零时的速率为 |