题目内容
【题目】如图所示，绝缘光滑轨道的仙部分为倾角
=
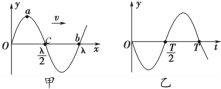
的斜面，AC部分为竖直平面内半径为R的半圆轨道，斜面与半圆轨道相切于A点，E为轨道的最低点，整个装置处于水平向右的恒定风力场（小球在风力场中受风力恒定）中。现有一个质量为m的小球，从斜面上某点由静止释放，当小球通过C点时所受合力的方向指向圆心，且小球对轨道的压力恰好为零。已知重力加速度大小为g，求：
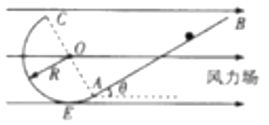
（1）小球受到风力的大小和到达C点时速度的大小；
（2）小球到达E点时动能的大小；
（3）小球通过C点后至落到轨道所用的时间。
【答案】（1）
（2）(
+1)mg（3）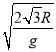
【解析】
(1)小球运动到C点时，由受到的重力和向右的风力提供向心力，则有：
tan
解得
F=
mg
而
解得
(2)小球由E点到C点过程，根据动能定理有
解得
Ek=(+1)mg
(3)小球离开C点后将做类似平抛运动，落到斜面上时有：
2R=
at2
而
联立解得
t=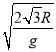
练习册系列答案
相关题目
