题目内容
某同学在物理学习中记录了一些与地球、月球有关的数据资料如下:地球半径R=6400km,月球半径r=1740km,地球表面重力加速度g=9.80m/s2,月球表面重力加速度g′=1.56m/s2,月球绕地球中心转动的线速度v=l km/s,月球绕地球转动一周时间为T=27.3天,光速c=2.998×105km/s.1969年8月1日第一次用激光器向位于头顶的月球表面发射出激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号,利用上述数据可估算出地球表面与月球表面之间的距离s,则下列方法正确的是( )A.利用激光束的反射s=c?
 来算
来算B.利用v=
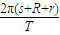 来算
来算C.利用m月g=m月
 来算
来算D.利用m月g′=m月
 (s+R+r)来算
(s+R+r)来算
【答案】分析:由题,激光光束从发射到接收的时间为t=2.565s,则激光光束从地球射到月球的时间为 ,光速为c,地球表面与月球表面之间的距离s=c?
,光速为c,地球表面与月球表面之间的距离s=c? .月球中心绕地球中心圆周运动的线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v=
.月球中心绕地球中心圆周运动的线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v= (s+R+r)可以求出s.月球所在处重力加速度不等于g和g′,月球绕地球圆周运动的向心力不等于mg和mg′.
(s+R+r)可以求出s.月球所在处重力加速度不等于g和g′,月球绕地球圆周运动的向心力不等于mg和mg′.
解答:解:A、由题,激光光束从地球射到月球的时间为 ,则地球表面与月球表面之间的距离s=c?
,则地球表面与月球表面之间的距离s=c? .故A正确.
.故A正确.
B、月球绕地球中心做匀速圆周运动,其线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v= (s+R+r)可以算出s.故B正确.
(s+R+r)可以算出s.故B正确.
C、月球的向心力由其重力提供,而月球所在处的重力不等于月球在地球表面的重力m月g.故C错误.
D、g′是月球表面的重力加速度,不是月球绕地球圆周运动的加速度,不能用来求月球的向心力.故D错误.
故选AB
点评:本题是实际问题,要抽象成物理模型,即月球绕地球做匀速圆周运动,其向心力由月球的重力提供.
 ,光速为c,地球表面与月球表面之间的距离s=c?
,光速为c,地球表面与月球表面之间的距离s=c? .月球中心绕地球中心圆周运动的线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v=
.月球中心绕地球中心圆周运动的线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v= (s+R+r)可以求出s.月球所在处重力加速度不等于g和g′,月球绕地球圆周运动的向心力不等于mg和mg′.
(s+R+r)可以求出s.月球所在处重力加速度不等于g和g′,月球绕地球圆周运动的向心力不等于mg和mg′.解答:解:A、由题,激光光束从地球射到月球的时间为
 ,则地球表面与月球表面之间的距离s=c?
,则地球表面与月球表面之间的距离s=c? .故A正确.
.故A正确.B、月球绕地球中心做匀速圆周运动,其线速度大小为v,月球中心到地球中心的距离为s+R+r,由公式v=
 (s+R+r)可以算出s.故B正确.
(s+R+r)可以算出s.故B正确.C、月球的向心力由其重力提供,而月球所在处的重力不等于月球在地球表面的重力m月g.故C错误.
D、g′是月球表面的重力加速度,不是月球绕地球圆周运动的加速度,不能用来求月球的向心力.故D错误.
故选AB
点评:本题是实际问题,要抽象成物理模型,即月球绕地球做匀速圆周运动,其向心力由月球的重力提供.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
近年来,因中国的“嫦娥探月”、美国的火箭撞月、印度的“月船一号”等让公众重新燃起了对月球的激情.某同学在物理学习中记录了一些与地球、月球有关的数据资料为:地球半径R=6400km,月球半径r=1740km,地球表面重力加速度g0=9.80m/s2,月球表面重力加速度g′=1.56m/s2,月球绕地球转动的线速度v=1000m/s,月球绕地球转动一周的时间T=27.3天,光速c=2.998×105km/s,假设某次实验中用激光器向位于头顶正上方的月球表面发射出的激光光束,经过约t=2.565s接收到从月球表面发射回来的激光信号,利用上述数据可算出地球表面与月球表面之间的距离s,则下列方法正确的是( )
A、利用激光束的发射,用s=cg
| ||
B、利用月球运动的线速度及周期关系v=
| ||
C、利用地球表面的重力加速度、地球半径及月球运动的 线速度关系m月g0=m月
| ||
D、利用月球表面的重力加速度、地球半径及月球运动周期关系m月g′=m月
|
 来算
来算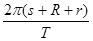 来算
来算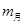 g0=
g0= 来算
来算 =
=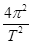 (s+R+r)来算
(s+R+r)来算