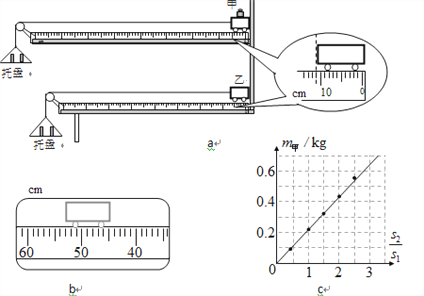
题目内容
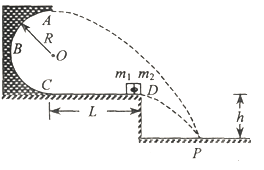
【题目】如图所示,半径![]() 的光滑半圆轨道竖直固定在高
的光滑半圆轨道竖直固定在高![]() 的光滑水平台上并与平台平滑连接。平台上有一用水平轻质细线栓接的物块
的光滑水平台上并与平台平滑连接。平台上有一用水平轻质细线栓接的物块![]() 和
和![]() 组成的装置
组成的装置![]() ,装置
,装置![]() 中两物块之间有一处于压缩状态的轻质小弹簧(物块与弹簧不栓接),
中两物块之间有一处于压缩状态的轻质小弹簧(物块与弹簧不栓接),![]() 处于静止状态。某时刻给装置
处于静止状态。某时刻给装置![]() 一个瞬时冲量使
一个瞬时冲量使![]() 和
和![]() 获得一个共同的初速度,同时由于扰动细线断开,待弹簧恢复原长后,
获得一个共同的初速度,同时由于扰动细线断开,待弹簧恢复原长后,![]() 、
、![]() 两物块获得方向相反的水平速度,
两物块获得方向相反的水平速度,![]() 沿半圆轨道运动并恰好到达半圆轨道的最高点
沿半圆轨道运动并恰好到达半圆轨道的最高点![]() ,
,![]() 沿平台运动并落在距平台边缘水平距离
沿平台运动并落在距平台边缘水平距离![]() 的地面上的
的地面上的![]() 点。已知
点。已知![]() ,
,![]() ,不计空气阻力,
,不计空气阻力,![]() 取
取![]() 。求:
。求:
(![]() )弹簧恢复原长时物块
)弹簧恢复原长时物块![]() 和
和![]() 分别获得的速度大小;
分别获得的速度大小;
(![]() )弹簧最初被压缩时所具有的弹性势能。
)弹簧最初被压缩时所具有的弹性势能。
【答案】(1)5m/s;4m/s(2)2.7J
【解析】(1)m1沿半圆轨道运动并恰好到达半圆轨道的最高点A时,由重力提供向心力,则有:![]()
m1从C到A的过程,由机械能守恒定律得:![]()
可得m1获得的速度大小为:v1=5m/s
m2离开平台后做平抛运动,则有:![]()
![]()
解得m2获得的速度大小为:v2=4m/s
(2)设原来系统的初速度为v0.取向右为正方向,根据动量守恒定律得:
(m1+m2)v0=-m1v1+m2v2.
根据系统的机械能守恒得:![]()
联立解得:Ep=2.7J

练习册系列答案
相关题目