题目内容
【题目】如图所示，AB是固定在竖直平面内半径为R的
光滑圆形轨道，轨道在最低点B与水平粗糙轨道BC平滑连接，BC的长度为2R．一质量为m的物块Q静止放置在水平轨道上与B点相距为x处．另一质量也为m的物块P从A点无初速释放，沿轨道下滑后进入水平轨道并与Q发生完全非弹性碰撞．已知两物块与水平轨道间的动摩擦因数均为μ=0.25，两物块都可视为质点，重力加速度为g．
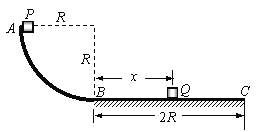
（1）求P刚要到达B点时受到轨道的支持力的大小．
（2）若两物块碰撞后能越过C点，求x与R之间应满足的关系．
（3）讨论物块P和物块Q在水平轨道运动过程克服摩擦力做的总功Wf与x和R之间的关系．
【答案】（1）
（2）
（3）
【解析】（1）P刚要到达B时速度为v0，由机械能守恒定律得： 
… ①
由牛顿定律得： 
…②
联立①②解得P受到轨道的支持力大小F=3mg…③
（2）P沿水平轨道滑行至碰到Q前速度为v1，由动能定理得： 
…④
设P、Q碰撞后的共同速度为v2，由动量守恒定律得：mv1=2mv2…⑤
若P、Q恰好滑至C点停下，由动能定理得： 
联立解得： 
因此两物块碰撞后能越过C点，x与R之间应满足的关系为：x＞
R．
（3）讨论：
①x＞
R，物块碰撞后能越过C点，克服摩擦力做的总功Wf为：
Wf=μmgx+μ2mg（2R-x）
解得： 
②x≤
R，物体碰撞后最终停止在轨道上，克服摩擦力做的总功Wf为：
解得： 
练习册系列答案
相关题目
