��Ŀ����
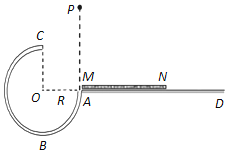
����Ŀ����ͼ��ʾ,һ���뾶ΪR���ķ�֮��Բ���ι⻬ϸԲ�ܹ��ABC�̶�����ֱƽ����,�����A����ˮƽ����AD���,������Բ��O�ȸ�.MN�Ƿ���ˮƽ�����ϳ���Ϊ2R����Ȳ��Ƶĵ���,���M����λ��A�㡣��һ������Ϊm��С��(����Ϊ�ʵ�)��A�����Ϸ���P���ɾ�ֹ�ͷţ����ƿ����������������ٶ�Ϊg.
(1)��С��ǡ���ܵ���ܿ�C��,��P��A����ĸ߶Ȳ�h1��
(2)��С��ӹܿ�C��ɳ���ǡ�ô�MN���е�,��P��A����ĸ߶Ȳ�h2��
(3)��P��A����ĸ߶Ȳ�Ϊh�����Ƶ���С���ܴ�MN��ǰ���£�����ܿ�C���С��ĵ���F�Ĵ�С��߶�h�ı仯��ϵʽ��
���𰸡�(1)0.4m(2)0.8m(3) ��0.5m��h��0.6mʱ��F��6-10h, ��0.6m��h��1.3mʱ��F��10h-6
����������1��С��ǡ���ܵ���ܿ�C���ٶ�Ϊ��
![]()
���![]()
��2��С��ӹܿ�C��ɳ���ǡ�ô�MN���е�
![]()
![]()
![]()
���![]()
��3����С��ܿ�C��ʱ��ܿ���������![]()
![]()
���![]()
С��ӹܿ�C��ɳ���ǡ�ô�A��
![]()
![]()
![]()
���![]()
��0.5m��h��0.6mʱ��F��6-10h
С��ӹܿ�C��ɳ���ǡ�ô�N��
![]()
![]()
![]()
���![]()
��0.6m��h��1.3mʱ��F��10h-6

��ϰ��ϵ�д�
�����Ŀ