题目内容
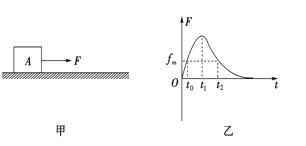
【题目】如图甲所示,在水平地面上固定一竖直轻弹簧,弹簧上端与一个质量为0.1kg的木块A相连,质量也为0.1kg的木块B叠放在A上,A、B都静止.在B上作用一个竖直向下的力F使木块缓慢向下移动,力F大小与移动距离x的关系如图乙所示,整个过程弹簧都处于弹性限度内.下列说法正确的是( )

A. 木块下移0.1m过程中,弹簧的弹性势能增加2.5J
B. 弹簧的劲度系数为500N/m
C. 木块下移0.1m时,若撤去F,则此后B能达到的最大速度为4m/s
D. 木块下移0.1m时,若撤去F,则A、B分离时的速度为5m/s
【答案】B
【解析】由图可知,F﹣x图象中,F与横坐标之间的“面积”表示力F做的功,所以这个过程中力F做功:![]() ,而弹簧弹性势能的增加量等于力F做的功与木块重力势能的减少量之和,故弹簧的弹性势能增加量大于2.5J,故A错误;弹簧的形变量增大0.1m的过程中,压力增大50N,根据胡克定律可得:
,而弹簧弹性势能的增加量等于力F做的功与木块重力势能的减少量之和,故弹簧的弹性势能增加量大于2.5J,故A错误;弹簧的形变量增大0.1m的过程中,压力增大50N,根据胡克定律可得:![]() ,故B正确;若撤去F,则A与B整体将以开始时的位置为平衡位置做简谐振动,所以当AB回到平衡位置时速度最大,由于开始阶段压力做功2.5J,所以A与B的速度最大时,二者动能的和是2.5J,即
,故B正确;若撤去F,则A与B整体将以开始时的位置为平衡位置做简谐振动,所以当AB回到平衡位置时速度最大,由于开始阶段压力做功2.5J,所以A与B的速度最大时,二者动能的和是2.5J,即![]() ,解得:vm=5m/s,故C错误;由C的分析可知,当B的速度是5m/s时,二者仍然在平衡位置,所以二者的加速度都等于0,B受到的A对B的弹力等于重力,所以二者没有分离,故D错误。所以B正确,ACD错误。
,解得:vm=5m/s,故C错误;由C的分析可知,当B的速度是5m/s时,二者仍然在平衡位置,所以二者的加速度都等于0,B受到的A对B的弹力等于重力,所以二者没有分离,故D错误。所以B正确,ACD错误。

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】下表是某同学为探究弹力和弹簧伸长的关系所测的几组数据:
弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
弹簧的伸长量x/cm | 2.6 | 5.0 | 6.8 | 9.8 | 12.4 |
(1)请你在图中的坐标线上作出F-x图象.

(2)写出曲线所代表的函数.(x用m作单位)
(3)解释函数表达式中常数的物理意义.
【题目】某实验小组利用拉力传感器和速度传感器探究“动能定理”.如图所示,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0 cm的A.B两点各安装一个速度传感器,记录小车通过A.B点时的速度大小,小车中可以放置砝码.

(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上,另一端通过定滑轮与钩码相连;正确连接所需电路.
②将小车由C点释放,小车在细线拉动下运动,记录细线拉力及小车通过A.B点时的速度.
③在小车中增加或减少砝码,重复②的操作.
在以上实验中,遗漏了 步骤。
(2)下列表格是他们用正确方法测得的一组数据,其中M是M1与小车中砝码质量M2之和,|v-v|是两个速度传感器记录速度的平方差,可以据此计算出动能变化量ΔE,F是拉力传感器测得的拉力,W是F在A.B间所做的功.表格中的ΔE3=_______,W3=______.(结果保留三位有效数字)
数据记录表
次数 | M/kg |
| ΔE/J | F/N | W/J |
1 | 0.500 | 0.76 | 0.190 | 0.400 | 0.200 |
2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
3 | 0.500 | 2.40 | ΔE3 | 1.220 | W3 |
4 | 1.000 | 2.40 | 1.200 | 2.420 | 1.210 |
5 | 1.000 | 2.84 | 1.420 | 2.860 | 1.430 |
(3)根据表格,请在图中的方格纸上作出ΔE—W图线.
(4)根据![]() 图线,可得 结论。
图线,可得 结论。