Question

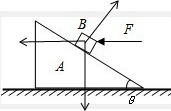
如图所示，A是质量为M、斜面倾角为θ的光滑楔形木块，静置在光滑水平面上．小滑块B的质量为m，今用一水平力推小滑块，使小滑块和楔形木块保持相对静止．则该水平力的大小为

F=（M+m）

mgtanθ

M

．

Answer 1

分析：先以木块和小滑块整体为研究对象根据牛顿第二定律列方程求出加速度大小，
然后对木块受力分析，根据牛顿第二定律列方程即可求解．

解答：解：以木块和小滑块整体为研究对象有：
F=（M+m）a
得：a=

F

m+M

①
对木块受力分析，如图：
根据牛顿第二定律，水平方向有：
F-Nsinθ=ma②
又N=mgcosθ+Fsinθ③
联立得：F=

mgtanθ

M

（m+M）
故答案为：

mgtanθ

M

（m+M）

点评：本题考查了牛顿第二定律的应用，整体法与隔离法的间隔应用是关键．