题目内容
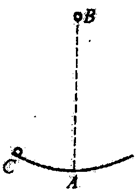
 如图所示,A是半径为r的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A,B,C质量相等.现给小球一水平向右的初速度v0,使小球在圆型轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足( )(重力加速度为g)
如图所示,A是半径为r的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A,B,C质量相等.现给小球一水平向右的初速度v0,使小球在圆型轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足( )(重力加速度为g)A、最小值为
| ||
B、最大值为
| ||
C、最小值为
| ||
D、最大值为
|
分析:小球在环内侧做圆周运动,通过最高点速度最小时,轨道对球的最小弹力为零,根据牛顿第二定律求出小球在最高点的最小速度;为了不会使环在竖直方向上跳起,小球在最高点对轨道的弹力不能大于2mg,根据牛顿第二定律求出最高点的最大速度,再根据机械能守恒定律求出小球在最低点的速度范围.
解答:解:在最高点,速度最小时有:mg=m
,解得:v1=
.
根据机械能守恒定律,有:2mgr+
mv12=
mv1′2,解得:v1′=
.
在最高点,速度最大时有:mg+2mg=m
,解得:v2=
.
根据机械能守恒定律有:2mgr+
mv22=
mv2′2,解得:v2′=
.
所以为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足:
≤v0≤
.故CD正确,A、B错误.
故选:CD.
| ||
| r |
| gr |
根据机械能守恒定律,有:2mgr+
| 1 |
| 2 |
| 1 |
| 2 |
| 5gr |
在最高点,速度最大时有:mg+2mg=m
| ||
| r |
| 3gr |
根据机械能守恒定律有:2mgr+
| 1 |
| 2 |
| 1 |
| 2 |
| 7gr |
所以为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足:
| 5gr |
| 7gr |
故选:CD.
点评:本题综合考查了牛顿第二定律和机械能守恒定律,关键理清在最高点的两个临界情况,求出在最高点的最大速度和最小速度.

练习册系列答案
相关题目