��Ŀ����
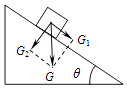
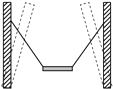
����Ŀ����ͼ����ˮƽ�棨���ߣ�֮��ľ���ΪH������������ڷ���ˮƽ���ҵ���ǿ�糡���Ը������Ϸ���A�㽫����Ϊm��������ֱ�Ϊq�ͩ�q��q��0���Ĵ���С��M��N�Ⱥ�����ͬ�ij��ٶ���ƽ���ڵ糡�ķ��������С�������������½���糡�����Ӹ�������±߽��뿪����֪N�뿪�糡ʱ���ٶȷ�����ֱ���£�M�ڵ糡����ֱ���˶������뿪�糡ʱ�Ķ���ΪN���뿪�糡ʱ�Ķ��ܵ�1.5�������ƿ����������������ٶȴ�СΪg����
��1��M��N�ڵ糡����ˮƽ�����λ��֮�ȣ�
��2��A���糡�ϱ߽�ĸ߶ȣ�
��3���õ糡�ĵ糡ǿ�ȴ�С��
���𰸡�
��1��
������С��ĵ�����ͬ����֪M���ڵ糡��ˮƽ���������ȼ���ֱ���˶���N����ˮƽ���������ȼ���ֱ���˶���ˮƽ�����ϵļ��ٶȴ�С��ȣ�
��������ֱ���������������ֱ�����������ٶ�Ϊg���ȼ���ֱ���˶���������ֱ�����ϵ�λ����ȣ����˶���ʱ����ȣ�
��ˮƽ����ļ��ٶȴ�СΪa��
��M���� ![]() ��
��
��N��v0=at�� ![]() ��
��
�ɵ� ![]() ��
��
���xM��xN=3��1��
�� M��N�ڵ糡����ˮƽ�����λ��֮��Ϊ3��1
��2��
������С���뿪�糡ʱ����ֱ���ٶ�Ϊvy��ˮƽ���ٶ�Ϊv1�������뿪�糡ʱ��ֱ���ٶ���ȣ�
��ΪM�ڵ糡����ֱ���˶������뿪�糡ʱ�Ķ���ΪN���뿪�糡ʱ�Ķ��ܵ�1.5�������У� ![]() ��
��
��� ![]() ��
��
��Ϊv1=v0+at=2v0���� ![]() =2v0��
=2v0��
��ΪM��ֱ���˶�����С����糡ʱ����ֱ�����ϵķ��ٶ�Ϊvy1�����У� ![]() �����vy1=
�����vy1= ![]() ��
��
����ֱ�������У� ![]() ��
�� ![]() ��
��
���A���糡�ϱ߽�ĸ߶�h= ![]() ��
��
��A���糡�ϱ߽�ĸ߶�Ϊ ![]() ��
��
��3��
��ΪM��ֱ���˶��������������ٶȷ�����ͬһ��ֱ���ϣ�
�У� ![]() =
= ![]() ��
��
��糡�ĵ糡ǿ��E= ![]() =
= ![]() ��
��
�𣺸õ糡�ĵ糡ǿ�ȴ�СΪ ![]() ��
��
����������1��ץס�����ڵ糡�У�ˮƽ�����ϵļ��ٶȴ�С��ȣ�һ�����ȼ���ֱ���˶���һ�����ȼ���ֱ���˶�������ֱ�����ϵ��˶�ʱ����ȵó�ˮƽ����ʱ����ȣ�����˶�ѧ��ʽ���M��N�ڵ糡����ˮƽ�����λ��֮�ȣ�
��2�������뿪�糡ʱ���ܵĴ�С��ϵ��ץסM��ֱ���˶����ó�M�뿪�糡ʱˮƽ���ٶȺ���ֱ���ٶȵĹ�ϵ��ץסM�ٶȷ��䣬��Ͻ���糡ʱ��ֱ���ٶȺ�ˮƽ���ٶȵĹ�ϵ�������ٶ�λ�ƹ�ʽ���A���糡�ϱ߽�ĸ߶ȣ�
��3����ϴ���С��M�糡����ֱ���˶�������ٶȷ���ó��糡���������Ĺ�ϵ���Ӷ�����糡ǿ�ȵĴ�С��