��Ŀ����
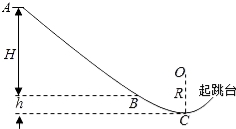
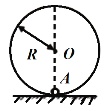
����Ŀ����ͼ��ʾ���뾶ΪR���ڱڹ⻬Բ�����ֱ�̶��������ϣ�һ������Ϊ�ʵ������Ϊm��С��ֹ�ڹ���ײ�A�㡣����С����ˮƽ������ٻ���С��ʹС���ڼ��̵�ʱ���ڻ��һ��ˮƽ�ٶȺ��ع������ֱ�����˶�����С��ص�A��ʱ���ٴ���С�����˶��������С��ͨ�����λ���С������˶���Բ�������ߵ㡣��֪С�����˶�������ʼ��δ���������ڵ�һ�λ��������С����С������W1���ڶ��λ��������С����С������W2�����Ⱥ����λ��������С����С������ȫ����������С��Ķ��ܣ���![]() ��ֵ�������� ��
��ֵ�������� ��
A��![]() B��
B��![]() C��
C��![]() D��1
D��1
���𰸡�BC
��������
�����������һ�λ��������ൽ��������O�ȸ�λ�ã����ݹ��ܹ�ϵ���У�W1��mgR����
���λ������Ե������ߵ㣬���ݹ��ܹ�ϵ���У�W1+W2-2mgR=![]() mv2����
mv2����
����ߵ㣬�У�mg+N=m![]() ��mg����
��mg����
�����٢ڢ۽�ã�W1��mgR��W2��![]() mgR
mgR
��![]() ����BC��ȷ��AD����ѡBC��
����BC��ȷ��AD����ѡBC��

��ϰ��ϵ�д�
�����Ŀ