题目内容
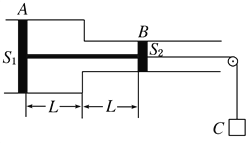
【题目】如图所示,足够长的宽为L=0.1m的导轨置于水平面上,左端接有一个电动势为E=1.5V,内阻为r=1.5Ω的电源,右端接有一个降压限流器件(当电路电流大于等于0.5A时相当于一个可变电阻而保持电流恒为0.5A,电流不能达0.5A时不起作用)和一个定值电阻R=0.4Ω,其它电阻不计,PQ是分界线且与左右两端足够远,导轨间有垂直导轨平面的匀强磁场。导轨在P点有一个小缺口,不计电阻的金属杆ab质量为m=0.01kg、从距PQ足够远处由静止释放,在PQ的左端它与导轨间的动摩擦因数为μ=0.2.在PQ的右端,它与导轨间无摩擦。金属杆到达PQ之前已经匀速运动且电源有最大输出功率。求:
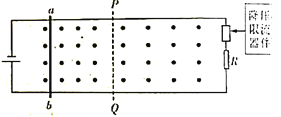
(1)磁感应强度B的大小;
(2)金属杆越过PQ前的最大加速度和最大速度;
(3)若金属杆越过PQ时,由于缺口的影响导致杆的速度立即减为原来速度的48%,金属杆还能运动的距离和通过R的电荷量。
【答案】(1)0.4T(2)18.75 m/s(3)2.25C
【解析】(1)电源达最大输出功率时,内外电压相等,电流的大小为I=![]()
由F=BLl=μmg可得:B=![]() =
=![]() =0.4T
=0.4T
(2)释放瞬间的加速度最大: ![]() =2m/s2(其中
=2m/s2(其中![]() )
)
金属杆匀速运动时的速度最大,设为v0
![]()
![]() =18.75 m/s
=18.75 m/s
(3)越过PQ后速度变为v1=0.48 v0=9m/s
如果器件不起作用,电路电流为![]() =0.9A>0.5A,可见器件将起作用,直到速成减为
=0.9A>0.5A,可见器件将起作用,直到速成减为
![]() =5m/s为止,此过程中,棒中电流I1=0.5A
=5m/s为止,此过程中,棒中电流I1=0.5A
从v1到v2金属杆做匀减速运动![]() =2m/s2
=2m/s2
![]() =2s
=2s
位移x1= v1 t1-![]() a t12=l4m
a t12=l4m
通过的电荷量q1=It1=1C
接下来将做变速速运动,依动量定理有: ![]()
x=12.5m
![]() =1.25C
=1.25C
x= x1+ x2 =26.5m
q= q1+q2 =2.25C

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案