题目内容
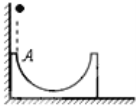
【题目】水平面上静止着两个大小可忽略的物块A和B，B质量是A质量的4倍，A与水平面间滑动摩擦系数μ=0.3，B与水平面间无摩擦力，B与右侧竖直挡板间距离s=0.5m，现在给A一水平初速度，A与B碰撞瞬间，A的速度v0=5m/s，A、B两物块发生弹性正碰，B与挡板碰撞时无机械能损失，不计碰撞时间，重力加速度g=10m/s2 ，则：两物体相碰后经多长时间再次相碰？
【答案】1.25s
【解析】
A、B两物块发生弹性正碰，动量守恒，机械能守恒，解得A与B碰撞后A的速度和B的速度，A与B碰撞后，A做匀减速直线运动，B做匀速运动，根据A与B的位移关系求出两物体相碰后再次相碰的时间；
解：设A的质量为m，B的质量为4m，设A与B碰撞后A的速度为v1，B的速度为v2，根据动量守恒可得：
A、B两物块发生弹性正碰，机械能守恒，则有：
解得
，
A与B碰撞后，A做匀减速直线运动，B做匀速运动
A的加速度大小为
，
A减速运动的时间为
A的减速位移为
B追上A运动的时间为
，所以两物体再次相碰时A已停止，故两物体相碰后经1.25s再次相碰
练习册系列答案
相关题目
