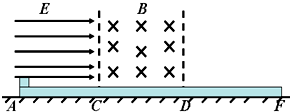
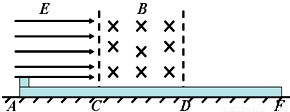
题目内容
 质量为M=150g的长木板静止放在光滑的水平面上,在长木板的上方有如图所示的匀强电场和匀强磁场,E=2N/C,B=1.25T,AC段是光滑的,CDF段滑动摩擦因数?=0.5,CD段的长度L=0.8m,质量为m=50g、电量为q=+0.1C的小物块,在A点静止释放,小物块始终在木板上运动,当小物块运动到D点时,木板才开始运动,最后小物块恰好未从木板上掉下.在运动过程中小物块电量不变.求
质量为M=150g的长木板静止放在光滑的水平面上,在长木板的上方有如图所示的匀强电场和匀强磁场,E=2N/C,B=1.25T,AC段是光滑的,CDF段滑动摩擦因数?=0.5,CD段的长度L=0.8m,质量为m=50g、电量为q=+0.1C的小物块,在A点静止释放,小物块始终在木板上运动,当小物块运动到D点时,木板才开始运动,最后小物块恰好未从木板上掉下.在运动过程中小物块电量不变.求(1)小物块在CD段的运动速度;
(2)AC段的长度;
(3)小物块在木板上相对木板的滑动的时间.
分析:本题的关键是通过分析得出小物块在CD段做匀速直线运动,再根据重力等于洛伦兹力求出在CD段的速度,然后用动能定理求出AC段的长度,再分别对小物块和木板受力分析,结合牛顿第二定律及运动学公式求出运动时间.
解答:解:(1)由题意可知小物块在CD段做匀速直线运动,由mg=qvB得,v=4m/s
故小物块在CD段的运动速度为4m/s.
(2)小物块在AC段由动能定理qE
=
m
-0,解得
=2m
即AC段长度为2m.
(3)小物块在AC段时间由v=
,可得
=1s
小物块在CD段时间由L=v
得,
=0.2s
小物块在DF段,设时间
,与木板共同速度为
,对小物块有
=μg=5m/
,所以
=v-
=4-5
,
对长木板有
=
=
m/
,所以
=
=
,
联立可得
=0.6s,所以总时间t=
=1.8s
即小物块在木板上相对木板的滑动时间为1.8s.
故小物块在CD段的运动速度为4m/s.
(2)小物块在AC段由动能定理qE
| L | AC |
| 1 |
| 2 |
| v | 2 |
| L | AC |
即AC段长度为2m.
(3)小物块在AC段时间由v=
| 1 |
| t | 1 |
小物块在CD段时间由L=v
| t | 2 |
| t | 2 |
小物块在DF段,设时间
| t | 3 |
| v | 共 |
| a | 1 |
| s | 2 |
| v | 共 |
| 3 |
| t | 3 |
对长木板有
| a | 2 |
| μmg |
| M |
| 5 |
| 3 |
| s | 2 |
| v | 共 |
| a | 2 |
| t | 3 |
| 3 |
联立可得
| t | 3 |
| t | 1 |
| +t | 2 |
| +t | 3 |
即小物块在木板上相对木板的滑动时间为1.8s.
点评:求解物理题的关键是物理过程分析和受力分析,根据不同的过程列出相应方程求解即可.

练习册系列答案
相关题目
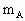 =150g,
=150g,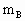 =50g,一质量为m=10g的子弹以
=50g,一质量为m=10g的子弹以 =500m/s的速度水平射入木块,先穿透A,接着穿透B,速度变为100m/s,假定子弹射穿A和B的时间相同,子弹所受的阻力相同.求:
=500m/s的速度水平射入木块,先穿透A,接着穿透B,速度变为100m/s,假定子弹射穿A和B的时间相同,子弹所受的阻力相同.求: