题目内容
9.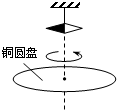 1824年,法国科学家阿拉果完成了著名的“圆盘实验”.实验中将一铜圆盘水平放置,在其中心正上方用柔软细线悬挂一枚可以自由旋转的磁针,如图所示.实验中发现,当圆盘在磁针的磁场中绕过圆盘中心的竖直轴旋转时,磁针也随着一起转动起来,但略有滞后.下列说法正确的是( )
1824年,法国科学家阿拉果完成了著名的“圆盘实验”.实验中将一铜圆盘水平放置,在其中心正上方用柔软细线悬挂一枚可以自由旋转的磁针,如图所示.实验中发现,当圆盘在磁针的磁场中绕过圆盘中心的竖直轴旋转时,磁针也随着一起转动起来,但略有滞后.下列说法正确的是( )| A. | 圆盘上产生了感应电动势 | |
| B. | 圆盘内的涡电流产生的磁场导致磁针转动 | |
| C. | 在圆盘转动的过程中,磁针的磁场穿过整个圆盘的磁通量发生了变化 | |
| D. | 圆盘中的自由电子随圆盘一起运动形成电流,此电流产生的磁场导致磁针转动 |
分析 通过题意明确涡流的产生,再根据磁极和电流间的相互作用分析磁铁的运动.
解答 解:A、圆盘在转动中由于半径方向的金属条切割磁感线,从而在圆心和边缘之间产生了感应电动势;故A正确;
B、圆盘在径向的金属条切割磁感线过程中,内部距离圆心远近不同的点电势不等,从而形成涡流,涡流产生的磁场又导致磁针转动,故B正确;
C、由于圆盘面积不变,距离磁铁的距离不变,故整个圆盘中的磁通量没有变化;故C错误;
D、电流形成是自由电子定向移动.圆盘本身没有多余的电荷,圆盘转动不会产生电流;故D错误;
故选:AB.
点评 本题要注意明确电流的形成不是因为自由电子运动,而是由于圆盘切割磁感线产生了电动势,从而产生了涡流.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.两相邻匀强磁场区域的磁感应强度大小不同,方向平行,一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱磁场区域后,粒子的( )
| A. | 轨道半径减少,角速度增大 | B. | 轨道半径减少,角速度减少 | ||
| C. | 轨道半径增大,角速度增大 | D. | 轨道半径增大,角速度减少 |
1.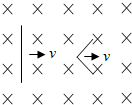 如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向运动时,棒两端的感应电动势大小为?;将此棒弯成两段长度相等且相互垂直的折线,置于与磁感应强度相垂直的平面内,当它沿两段折线夹角平分线的方向以速度v运动时,棒两端的感应电动势大小为?′.则$\frac{?′}{?}$等于( )
如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向运动时,棒两端的感应电动势大小为?;将此棒弯成两段长度相等且相互垂直的折线,置于与磁感应强度相垂直的平面内,当它沿两段折线夹角平分线的方向以速度v运动时,棒两端的感应电动势大小为?′.则$\frac{?′}{?}$等于( )
 如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向运动时,棒两端的感应电动势大小为?;将此棒弯成两段长度相等且相互垂直的折线,置于与磁感应强度相垂直的平面内,当它沿两段折线夹角平分线的方向以速度v运动时,棒两端的感应电动势大小为?′.则$\frac{?′}{?}$等于( )
如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向运动时,棒两端的感应电动势大小为?;将此棒弯成两段长度相等且相互垂直的折线,置于与磁感应强度相垂直的平面内,当它沿两段折线夹角平分线的方向以速度v运动时,棒两端的感应电动势大小为?′.则$\frac{?′}{?}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
18. P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )| A. | P1的平均密度比P2的大 | B. | P1的“第一宇宙速度”比P2的小 | ||
| C. | s1的向心加速度比s2的大 | D. | s1的公转周期比s2的大 |
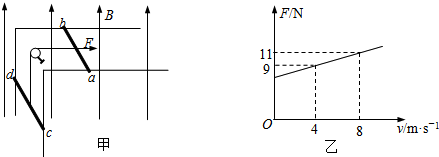

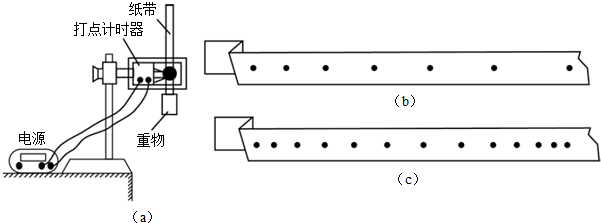
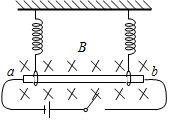 如图,一长为10cm的金属棒ab用两个完全相同的弹簧水平地悬挂在匀强磁场中,磁场的磁感应强度大小为0.1T,方向垂直于纸面向里,弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2Ω,已知开关断开时两弹簧的伸长量均为0.5cm,闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取10m/s2,判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量.
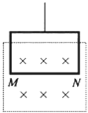
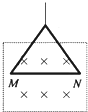
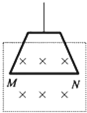
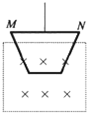
如图,一长为10cm的金属棒ab用两个完全相同的弹簧水平地悬挂在匀强磁场中,磁场的磁感应强度大小为0.1T,方向垂直于纸面向里,弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2Ω,已知开关断开时两弹簧的伸长量均为0.5cm,闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取10m/s2,判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量.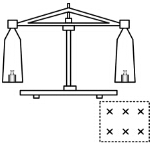 如图所示,用天平测量匀强磁场的磁感应强度,下列各选项所示的载流线圈匝数相同,边长MN相等,将它们分别挂在天平的右臂下方,线圈中通有大小相同的电流,天平处于平衡状态,若磁场发生微小变化,天平最容易失去平衡的是( )
如图所示,用天平测量匀强磁场的磁感应强度,下列各选项所示的载流线圈匝数相同,边长MN相等,将它们分别挂在天平的右臂下方,线圈中通有大小相同的电流,天平处于平衡状态,若磁场发生微小变化,天平最容易失去平衡的是( )