题目内容
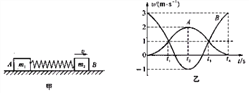
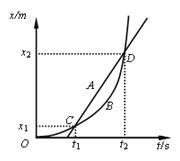
【题目】如图所示为A、B两质点在同一直线上运动的位移—时间(x-t)图象,A质点的图像为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图。下列说法不正确的是( )
A. A、B相遇两次
B. t1~t2时间段内B质点的平均速度与A质点匀速运动的速度相等
C. 两物体速度相等的时刻一定在t1~t2时间段内的中间时刻
D. A在B前面且离B最远时,B的位移为![]()
【答案】D
【解析】
图象的交点表示同一时刻到达同一位置而相遇,可知,A、B分别在t1和t2两个时刻相遇,故A正确;t1~t2时间段内,两质点通过的位移相等,则B质点的平均速度与A质点匀速运动的速度相等,故B正确。位移-时间图象斜率表示速度,B图线的切线斜率不断增大,而且B图线是抛物线,有x=kt2,则知B做匀加速直线运动。因为t1~t2时间段内,B质点的平均速度与A质点匀速运动的速度相等,而匀变速直线运动的平均速度等于这段时间内中间时刻的瞬时速度,所以两物体速度相等的时刻一定在t1~t2时间段内的中间时刻,故C正确。当AB速度相等时,相距最远,该时刻在t1~t2时间段内的中间时刻,由于B做匀加速直线运动,所以此时B的位移小于![]() ,故D错误。本题选不正确的,故选D。
,故D错误。本题选不正确的,故选D。

练习册系列答案
相关题目