题目内容
16. 如图所示,位于光滑水平桌面上的小滑块P和Q都可视作质点,P的质量是Q质量的4倍,Q与轻质弹簧相连.P、Q以相同的初动能相向运动,并且P与弹簧发生碰撞.在整个碰撞过程中,下列说法正确的是( )
如图所示,位于光滑水平桌面上的小滑块P和Q都可视作质点,P的质量是Q质量的4倍,Q与轻质弹簧相连.P、Q以相同的初动能相向运动,并且P与弹簧发生碰撞.在整个碰撞过程中,下列说法正确的是( )| A. | 弹簧具有的最大弹性势能等于P的初动能 | |
| B. | 弹簧具有的最大弹性势能等于P的初动能的1.8倍 | |
| C. | P的速度不可能为零 | |
| D. | P的速度可能为零 |
分析 P和Q相向运动并与弹簧发生碰撞的过程中,系统的动量守恒,当P、Q的速度相同时,弹簧的弹性势能最大,根据动量守恒和机械能守恒求解.
解答 解:A、设P的质量为4m,初速度为v0,Q的质量为m,根据P、Q初动能相等得:
$\frac{1}{2}×4m{{v}_{0}}^{2}=\frac{1}{2}m{v}^{2}$
解得:v=2v0
P和Q相向运动并与弹簧发生碰撞的过程中,当P、Q的速度相同时,弹簧的弹性势能最大,此过程中系统的动量守恒,机械能守恒,
以P的初速度方向为正方向,根据动量守恒定律得:
4mv0-2mv0=(4m+m)v′
解得:v$′=\frac{2}{5}{v}_{0}$
根据机械能守恒定律得:
$\frac{1}{2}×4m{{v}_{0}}^{2}×2=\frac{1}{2}×5mv{′}^{2}+{E}_{P}$
解得:EP=$\frac{18}{5}m{{v}_{0}}^{2}$=$\frac{1}{2}×4m{{v}_{0}}^{2}×1.8$,即弹簧具有的最大弹性势能等于P的初动能的1.8倍,故A错误,B正确;
C、若P点速度为0,根据动量守恒定律得:
4mv0-2mv0=mv1
解得:v1=2v0
此过程中,机械能守恒,则有:
$\frac{1}{2}×4m{{v}_{0}}^{2}×2=\frac{1}{2}m{{v}_{1}}^{2}+{E}_{P}$′
解得:${E}_{P}′=2m{{v}_{0}}^{2}$
满足条件,故P点速度可以为零,故C错误,D正确.
故选:BD
点评 本题是系统的动量守恒和机械能守恒的问题,关键要抓住速度相等时,弹簧的弹性势能最大这个临界条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.关于第一宇宙速度,下列说法正确的是( )
| A. | 它是人造地球卫星绕地球匀速圆周飞行的最大速度 | |
| B. | 它等于人造地球卫星在近地圆形轨道上的运行速度 | |
| C. | 它是能使卫星绕地运动的最小发射速度 | |
| D. | 它是卫星在椭圆轨道上运动时的近地点速度 |
4.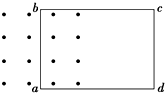 闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
 闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )| A. | 向左平动进入磁场 | B. | 向右平动进入磁场 | ||
| C. | 向上平动 | D. | 向下平动 |
11.如图所示,小球沿着光滑斜面①和光滑曲面 ②分别由静止释放,则( )


| A. | 小球两次到达底端时的速度大小相同 | |
| B. | 小球两次到达斜面底端时重力的瞬时功率相同 | |
| C. | 从开始运动到落地过程中重力做功相同 | |
| D. | 从开始运动到落地过程中重力的平均功率$\overline{{P}_{1}}$>$\overline{{P}_{2}}$ |
1.分别标有“220V,40W“和“220V,60W“字样的甲、乙两盏电灯,若将它们串联起来仍接在220伏的电路中,则下列判断中正确的是( )
| A. | 甲灯亮些 | B. | 乙灯亮些 | C. | 两灯一样亮 | D. | 无法判定 |
5. 如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
 如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )| A. | 着地时两物体速度相同 | B. | 着地时两物体机械能相同 | ||
| C. | 着地时两物体所受重力的功率相同 | D. | 两物体沿斜面滑行的时间相同 |

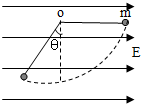 两平行板间有水平匀强电场,一根长为L,不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,求:(θ=37°且sin37°=$\frac{3}{5}$ cos37°=$\frac{4}{5}$)
两平行板间有水平匀强电场,一根长为L,不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,求:(θ=37°且sin37°=$\frac{3}{5}$ cos37°=$\frac{4}{5}$)