��Ŀ����
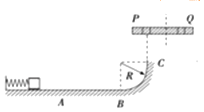
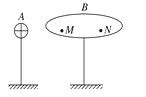
����Ŀ����ͼ��ʾ����ֱ��������һ���۵�Բ��ˮƽ���ã����ƹ�����O�����ֱ��ת������������һ�����ʵ��ɣ�����һ�˹̶���O�㣬��һ����������Ϊm��С���飮���ɵľ���ϵ��Ϊk��ԭ��Ϊl0 �� Բ�̰뾶Ϊ3l0 �� �۵���С�����Ķ��ϲ�������= ![]() �����۲���⻬��Բ�̿�ʼת��ʱ�����ɴ���ԭ��l0 �� ��֪�������ٶ�Ϊg�����Ħ�������ڻ���Ħ����������ʼ���ڵ������ڣ�����Բ��ת�������У�
�����۲���⻬��Բ�̿�ʼת��ʱ�����ɴ���ԭ��l0 �� ��֪�������ٶ�Ϊg�����Ħ�������ڻ���Ħ����������ʼ���ڵ������ڣ�����Բ��ת�������У�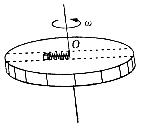
��1����Ҫʹ���ɲ������α䣬��Բ��ת���Ľ��ٶȱ��������������
��2�������ɳ���Ϊ2l0ʱ����С�����ܵ���Ħ����ǡ��Ϊ�㣬���ʱ����Ķ��ܣ�
��3�������ɳ���Ϊijһֵ1ʱ���������Բ�̾�ֹʱ�Ķ��ܿ���һ����Χ�ڱ仯���ñ仯�����ڶ��ܵ�����ֵ��Ϊ�������С����á�Ek��ʾ����ͨ������д���������С���Ek�뵯�ɳ���l��Ĺ�ϵʽ��
���𰸡�
��1��
���Ħ�����ṩ������ʱ��ʱ�Ľ��ٶ���ʦ�mg��m��2l0��
��ã� ![]() =
= ![]()
��Բ��ת���Ľ��ٶȱ������������Ϊ ![]() ��
��
��2��
�����ɳ���Ϊ2l0ʱ����С�����ܵ���Ħ����ǡ��Ϊ�㣬��ʱ���ɵĵ����ṩ���������� ![]() ����ʱ�Ķ���Ϊ��
����ʱ�Ķ���Ϊ�� ![]() ��
��
��ã� ![]()
�𣺴�ʱ����Ķ���Ϊ ![]() ��
��
��3��
�����ɳ���Ϊijһֵ1ʱ����ʱ���ɵĵ���F=k��l��l0�������ٶȽ�Сʱ���ܵ��ľ�Ħ����������Բ�ģ��� ![]() ��
��
��ʱ�Ķ���Ϊ�� ![]()
�����ٶȽϴ�ʱ����Ħ����ָ��Բ�ģ��� ![]() ��
��
��ʱ�Ķ���Ϊ�� ![]()
�ʡ������С���Ek�뵯�ɳ���l��Ĺ�ϵʽ ![]()
�� �������С���Ek�뵯�ɳ���l��Ĺ�ϵʽΪ ![]() ��
��
����������1�����Ħ�����ṩ������ʱ���ٶ������ţ�ٵڶ�������ã���2�����ɵĵ����պ��ṩ������������ţ�ٵڶ�������ã���3�������ɵij���Ϊlʱ���ٶȽ�С�ͽϴ������ܵ��ľ�Ħ����ָ��Բ�ĺͱ���Բ�ģ�����ţ�ٵڶ������������ٶȺ���С�ٶȣ�������ö�����
�����㾫����������Ĺؼ��������������������֪ʶ����������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�����������Լ��Զ��ܶ������ۺ�Ӧ�õ����⣬�˽�Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�