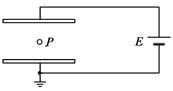
��Ŀ����
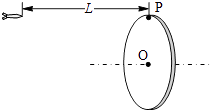
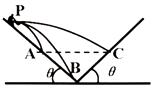
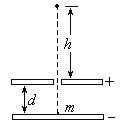
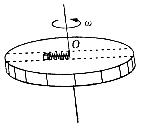
����Ŀ����ͼ��ʾ��һѹ�����ᵯ����˹̶����Ҷ���һ������Ӵ�����˩�ӣ���������Ϊm��A��������⻬��������ˮƽ����AB�μ�Ķ�Ħ������Ϊ0.2��AB�ij���Ϊ5R���ֽ������ɾ�ֹ�ͷţ������鱻����A��ʱ����ǡ�ָ�ԭ����֮�������B�㻬�У������Ϲ⻬�İ뾶ΪR�� ![]() �⻬Բ�����BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q��ƽ̨��תʱ�����ܴﵽC������Ϸ��������黬��C����P�״�������ǡ�ܴ�Q�״�����أ���֪ѹ�����ᵯ�ɾ��еĵ�������Ϊ4.5mgR�����������ɺ��Բ��ƣ���
�⻬Բ�����BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q��ƽ̨��תʱ�����ܴﵽC������Ϸ��������黬��C����P�״�������ǡ�ܴ�Q�״�����أ���֪ѹ�����ᵯ�ɾ��еĵ�������Ϊ4.5mgR�����������ɺ��Բ��ƣ���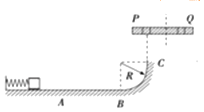
��1������ͨ��B��ʱ�Եذ��ѹ����
��2��ƽ̨ת���Ľ��ٶȦ�Ӧ����ʲô��������g��R��ʾ��
��3��С��������ͣ�ھ�A���Զ����������С����ÿ���뵯����ײʱû�л�е����ʧ��
���𰸡�
��1���⣺�����˶���B�Ĺ���ֻ�е��ɵ�����Ħ�������������ɶ��ܶ����ɵã� ![]() �����ԣ�
�����ԣ� ![]() ��
��
��ô���Ի�����B��Ӧ��ţ�ٵڶ����ɿɵã� ![]() ��
��
����ţ�ٵ������ɿɵã�����ͨ��B��ʱ�Եذ��ѹ��N=FN=8mg��
�𣺻���ͨ��B��ʱ�Եذ��ѹ��Ϊ8mg��
��2���⣺�����B��ƽ̨С�״����˶�����ֻ�������������ʻ�е���غ㣬���У� ![]() �����ԣ�������С�״����ٶ�
�����ԣ�������С�״����ٶ� ![]() ��
��
������С���Ϸ�ֻ�������������ʻ��鴩��P��Q��ʱ���� ![]() ��
��
ƽ̨ת���Ľ��ٶ� ![]() ��
��
��ƽ̨ת���Ľ��ٶ� ![]() ��
��
��3���⣺��С���ڶ��γ���BC����B�����ٶ�ΪvB�䣬��ô����С���Ӿ�ֹ��ʼ���˶�����Ӧ�ö��ܶ����ɵã� ![]() ��
��
�� ![]() ��С��鲻���ٴε���ƽ̨�߶ȣ�
��С��鲻���ٴε���ƽ̨�߶ȣ�
��ô��С��������˶������У�ֻ�е��ɵ�����Ħ�����������������AB��ͨ����·��Ϊx�����ɶ��ܶ����ɵã�Ep����mgx=0���� ![]() ��
��
���ԣ�С��������ͣ�ھ�A��2.5R����
��С��������ͣ�ھ�A��2.5R����
����������1�����ȣ����ݶ��ܶ������������B��ʱ���ٶ��ٸ�����������ʽ���ѹ����
��2����Ҫ��������Բ���˶��������ԡ�ʱ����ȷ����֪�ĵ���ת���ĽǶȲ�ȷ�������ݻ�е���غ������С��ʱ���ٶȣ����ݽ��ٶȶ�������⼴�ɡ�
��3���ȸ��ݶ��ܶ����ж�������������ĸ߶ȣ������ö��ܶ����ж��������յ�λ�á�
�����㾫����������Ĺؼ��������������������֪ʶ����������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�����������Լ��Զ��ܶ������ۺ�Ӧ�õ����⣬�˽�Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�