题目内容
4．
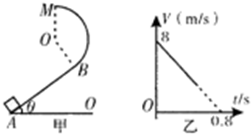如图甲所示，一半径为R=1m，竖直圆弧形光滑轨道，与斜面相切于B处，圆弧轨道的最高点为M，斜面倾角θ，t=0时刻，有一质量m=2kg的物块从A点开始沿斜面上滑，其在斜面上运动的速度变化规律如图乙所示．若物块恰能到达M点，求：（1）物块经过B点时的速度；
（2）物块在斜面上滑动的过程中克服摩擦力做的功．
分析 （1）物块恰能达到M点，由牛顿第二定律求出物块到达M点的速度，从B到M过程机械能守恒，由机械能守恒定律求出物块 经过B点速度速度．
（2）在斜面上求摩擦力的平均功率，首先由速度图象得出加速度和初速度，分析物块的受力，由牛顿第二定律求出摩擦力，由运动学公式求出位移，则由功的公式可求得克服摩擦力所做的功
解答 解：（1）由题中的几何关系可知，圆弧对应的圆心角为120°
物块从B到M上升的高度为：h=R+Rcos37°，
物块恰能过最高点，则在M点由牛顿第二定律得：mg=m$\frac{{v}_{M}^{2}}{R}$，
物块从B到M的过程中机械能守恒，由机械能守恒定律得：$\frac{1}{2}$mvB2=$\frac{1}{2}$mvM2+mgh，
联立以上各式解得物块经过B点时的速度为：vB=$\sqrt{46}$m/s；
（2）分析速度图象求知物块在斜面上的加速度为：a=$\frac{△v}{△t}$=$\frac{8}{0.8}$m/s2=10m/s2
在斜面上对物块由牛顿第二定律得：mgsinθ+f=ma，
摩擦力f=ma-mgsinθ=20-12=8N
对物块由vA2-vB2=2ax可得：x=0.9m；
则克服摩擦力的功W=fx=8×0.9=7.2J；
答：（1）物块经过B点时的速度vB为$\sqrt{46}$m/s；
（2）物块在斜面上滑动的过程中克服摩擦力做功为7.2J
点评 解答此题需结合速度图象分析物块从B到M和从A到B两过程的受力和运动特点，抓住在M点的临界条件：压力为零，然后利用几何关系、牛顿第二定律、机械能守恒定律求B点的速度．求摩擦力的功时由功的公式入手分析，求出对应的力和位移即可求得功．
练习册系列答案
相关题目
14．
如图所示，轻杆AB长l，两端各连接一个小球（可视为质点），两小球质量关系为mA=$\frac{1}{2}$mB=m，轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动．当轻杆转至水平位置时，A球速度为$\sqrt{\frac{2}{3}gl}$，则在以后的运动过程中（ ）
如图所示，轻杆AB长l，两端各连接一个小球（可视为质点），两小球质量关系为mA=$\frac{1}{2}$mB=m，轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动．当轻杆转至水平位置时，A球速度为$\sqrt{\frac{2}{3}gl}$，则在以后的运动过程中（ ）| A． | A球机械能守恒 | |
| B． | 当B球运动至最低点时，球A对杆作用力等于0 | |
| C． | 当B球运动到最高点时，杆对B球作用力等于0 | |
| D． | A球从图示位置运动到最低点的过程中，杆对A球做功等于0 |
12．
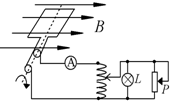如图所示，匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中，绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动，线框电阻不计，面积为0.4m2，线框通过滑环与一理想自耦变压器的原线圈相连，副线圈接有一只灯泡L（4W，100Ω）和滑动变阻器，已知图示状况下灯泡正常发光，电流表视为理想电表，则下列说法正确的是（ ）
如图所示，匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中，绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动，线框电阻不计，面积为0.4m2，线框通过滑环与一理想自耦变压器的原线圈相连，副线圈接有一只灯泡L（4W，100Ω）和滑动变阻器，已知图示状况下灯泡正常发光，电流表视为理想电表，则下列说法正确的是（ ）| A． | 此时原副线圈的匝数比为4：1 | |
| B． | 此时电流表的示数为0.4A | |
| C． | 若将自耦变压器触头向下滑动，灯泡会变暗 | |
| D． | 若将滑动变阻器滑片向上移动，则电流表示数增大 |
14．某大型商场的自动扶梯以恒定速率v1运送顾客上楼购物．某顾客第一次站在扶梯上不动随扶梯向上运动；第二次他以相对于扶梯的速率v2沿扶梯匀速向上走动．两次扶梯对这位顾客所做的功分别为W1和W2，扶梯牵引力的功率分别为P1和P2，则下列结论正确的是（ ）
| A． | W1＜W2，P1＜P2 | B． | W1＜W2，P1=P2 | C． | W1=W2，P1＜P2 | D． | W1＞W2，P1=P2 |